题目内容
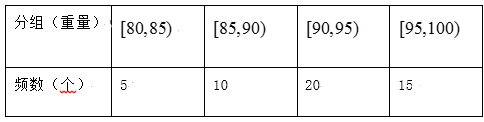
【题目】某市为广泛开展垃圾分类的宣传教育和倡导工作，使市民树立垃圾分类的环保意识，学会垃圾分类的知识，特举办了“垃圾分类知识竞赛".据统计，在为期1个月的活动中，共有两万人次参与网络答题.市文明实践中心随机抽取100名参与该活动的市民，以他们单次答题得分作为样本进行分析，由此得到如图所示的频率分布直方图：
（1）求图中a的值及参与该活动的市民单次挑战得分的平均成绩
(同一组中数据用该组区间中点值作代表)；
（2）若垃圾分类答题挑战赛得分落在区间
之外，则可获得一等奖奖励，其中，s分别为样本平均数和样本标准差，计算可得
，若某人的答题得分为96分，试判断此人是否获得一等奖；
（3）为扩大本次“垃圾分类知识竞赛”活动的影响力，市文明实践中心再次组织市民组队参场有奖知识竞赛，竞赛共分五轮进行，已知“光速队”与“超能队”五轮的成绩如下表：
成绩 | 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 |
“光速队” | 93 | 98 | 94 | 95 | 90 |
“超能队” | 93 | 96 | 97 | 94 | 90 |
①分别求“光速队”与“超能队”五轮成绩的平均数和方差；
②以上述数据为依据，你认为"光速队”与“超能队”的现场有奖知识竞赛成绩谁更稳定？
【答案】（1）
，
(分)；（2）此人未获得一等奖；（3）①“光速队”平均数为
，方差
，“超能队”平均数为，方差为
；②“超能队”的现场有奖知识竞赛成绩更稳定.
【解析】
（1）由各组的频率和为1求出a的值；平均成绩等于各组的中间值与其频率积的和；
（2）将（1）求出的平均值和
代入
，从而可判断96是否在此区间；
（3）①由表中的数据直接求平均数和方差即可；②比较两个方差的大小，方差小的成绩更稳定.
（1）由频率分布直方图可知
，解得；
参与该活动的市民单次挑战得分的平均值的平均成绩为
(分).
（2）由（1）知，区间
，而
，
故此人未获得一等奖；
（3）①“光速队”五轮成绩的平均数为
，
方差为
.
“超能队”五轮成绩的平均数为
，
方差为
.
②评价：从方差数据来看，“超能队”的现场有奖知识竞赛成绩更稳定.
