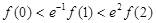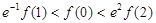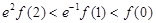题目内容
若存在过点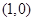 的直线与曲线
的直线与曲线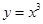 和
和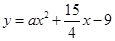 都相切,则
都相切,则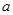 等于
等于
A.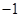 或 或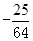 | B.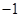 或 或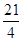 | C.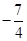 或 或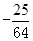 | D.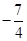 或 或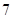 |
A
解析试题分析:由y=x3得到y'=3x2,设曲线y=x3上任意一点(x0,x03)处的切线方程为y-x03=3x02(x-x0),将(1,0)代入方程得x0=0或x0= ,
,
① 当x0=0时,切线方程为y=0,此直线是y=x3的切线,故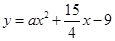 =0仅有一解,
=0仅有一解,
由△=0,解得a=-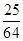 ;
;
② 当x0= 时,切线方程为y=
时,切线方程为y=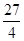 x-
x-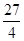 ,由
,由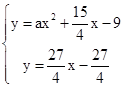
整理得,ax2-3x- =0,△=32-4a(-
=0,△=32-4a(- )=0,所以,a=-1,∴a=-1或a=-
)=0,所以,a=-1,∴a=-1或a=-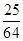 。故选A。
。故选A。
考点:本题主要考查导数的几何意义,直线方程,方程组的解法。
点评:典型题,本题是2009年江西高考题,综合性较强,对考生的思维能力、计算能力要求较高。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知二次函数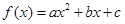 的导数为
的导数为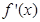 ,
,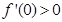 ,对于任意实数
,对于任意实数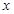 都有
都有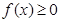 ,则
,则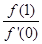 的最小值为 ( )
的最小值为 ( )
A.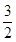 | B.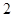 | C.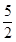 | D.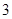 |
函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )
| A.1个 | B.2个 |
| C.3个 | D.4个 |
已知曲线y= x2-2上一点P
x2-2上一点P ,则过点P的切线的方程是( )
,则过点P的切线的方程是( )
A.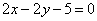 | B.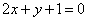 |
C.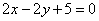 | D.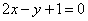 |
设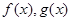 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当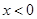 时,
时, 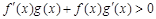 ,且
,且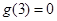 ,则不等式
,则不等式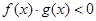 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0, 3) |
| C.(-∞,- 3)∪(3,+∞) | D.(-∞,- 3)∪(0, 3) |
已知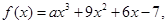 若
若 ,则a的值等于( )
,则a的值等于( )
A.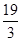 | B.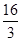 | C.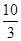 | D. |
一个物体的运动方程为 ,其中
,其中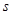 的单位是米,
的单位是米,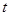 的单位是秒,那么物体在3秒末的瞬时速度是( )
的单位是秒,那么物体在3秒末的瞬时速度是( )
| A.3米/秒 | B.6米/秒 | C.5米/秒 | D.4米/秒 |
 是函数
是函数 的导函数,如果
的导函数,如果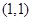 ,那么曲线
,那么曲线 的取值范围是
的取值范围是






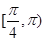
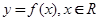 ,的导函数为
,的导函数为 ,且
,且 ,
, ,则下列不等式成立的是(注:e为自然对数的底数)( )
,则下列不等式成立的是(注:e为自然对数的底数)( )