题目内容
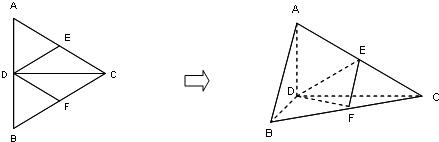
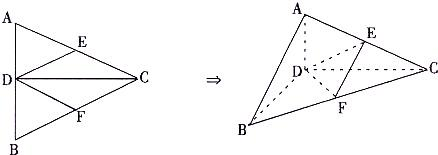
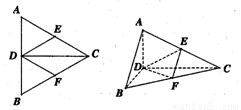
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B。
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E—DF—C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.

【答案】
解:(1)如图:在△ABC中,由E、F分别是AC、BC中点,得EF//AB,
又AB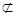 平面DEF,EF
平面DEF,EF 平面DEF. ∴AB∥平面DEF.
平面DEF. ∴AB∥平面DEF.
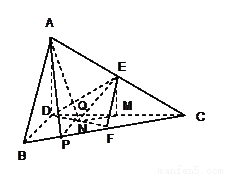
(2)∵AD⊥CD,BD⊥CD
∴∠ADB是二面角A—CD—B的平面角
∴AD⊥BD ∴AD⊥平面BCD
取CD的中点M,这时EM∥AD ∴EM⊥平面BCD
过M作MN⊥DF于点N,连结EN,则EN⊥DF
∴∠MNE是二面角E—DF—C的平面角
在Rt△EMN中,EM=1,MN=
∴tan∠MNE= ,cos∠MNE=
,cos∠MNE=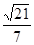
(3)在线段BC上存在点P,使AP⊥DE
证明如下:在线段BC上取点P。使 ,过P作PQ⊥CD与点Q,
,过P作PQ⊥CD与点Q,
∴PQ⊥平面ACD ∵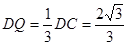 在等边△ADE中,∠DAQ=30°
在等边△ADE中,∠DAQ=30°
∴AQ⊥DE∴AP⊥DE
【解析】略

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目