题目内容
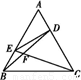
19、如图所示，正△ABC的边长为4，CD是AB边上的高，E、F分别是AC和BC的中点，现将△ABC沿CD翻折成直二面角A-DC-B．
（I）试判断翻折后直线AB与平面DEF的位置关系，并说明理由；
（II）求直线EF与平面ADC所成角的大小．
（I）试判断翻折后直线AB与平面DEF的位置关系，并说明理由；
（II）求直线EF与平面ADC所成角的大小．
分析：（I）由于E、F分别是AC和BC的中点，由三角形中位线定理，结合线面平行的判定定理，我们易判断出EF∥AB，进而得到直线AB∥平面DEF．
（II）根据面面垂直的定义，结合将△ABC沿CD翻折成直二面角A-DC-B，CD是AB边上的高，根据面面垂直的性质定理，易得BD⊥平面ADC，结合（I）中EF∥AB，易得∴∠BAD为直线EF与平面ADC所成角，解三角形后，即可得到答案．
（II）根据面面垂直的定义，结合将△ABC沿CD翻折成直二面角A-DC-B，CD是AB边上的高，根据面面垂直的性质定理，易得BD⊥平面ADC，结合（I）中EF∥AB，易得∴∠BAD为直线EF与平面ADC所成角，解三角形后，即可得到答案．
解答：解：（I）∵E、F分别是AC和BC的中点
∴EF∥AB
又EF?平面DEF，
AB?平面DEF
∴AB∥平面DEF（7分）
（II）∵二面角A-DC-B为直二面角，BD⊥CD
∴BD⊥平面ADC，
∵EF∥AB，
∴∠BAD为直线EF与平面ADC所成角．
∵AD=BD=2
∴∠BAD=45°即直线EF与平面ADC所成角为45°．（14分）
∴EF∥AB
又EF?平面DEF，
AB?平面DEF
∴AB∥平面DEF（7分）
（II）∵二面角A-DC-B为直二面角，BD⊥CD
∴BD⊥平面ADC，
∵EF∥AB，
∴∠BAD为直线EF与平面ADC所成角．
∵AD=BD=2
∴∠BAD=45°即直线EF与平面ADC所成角为45°．（14分）
点评：本题考查的知识点是空间中直线与平面之间的位置关系，直线与平面所成的角，其中熟练掌握线面平行的判定定理，线面垂直、线线垂直、面面垂直之间的相互转化及线面夹角的定义，是解答本题的关键．
练习册系列答案
相关题目
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为
AC,AE=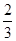
AB,BD,CE相交于点F.
