题目内容
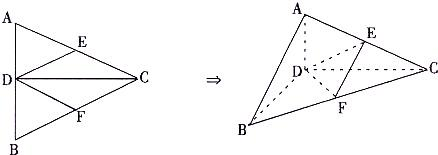
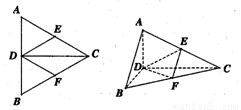
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B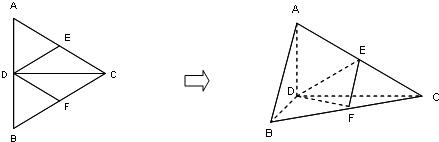
(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求二面角E-DF-C的余弦值;
(Ⅲ)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
分析:法一(1)要证明线面平行,关键是在平面内找到一条可能与已知直线平行的直线,观察到平面BEF中三条已知直线中,EF可能与AB平行,故可以以此为切入点进行证明.
(2)要求二面角的余弦,要先构造出二面角的平面角,然后利用解三角形的方法,求出这个平面角的余弦值,进而给出二面角的余弦值.
(3)线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.
法二,根据题意,构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法进行求解(1)利用直线的方向向量与平面的法向量之间的关系,判断线面关系,
(2)通过求两个平面法向量的夹角求二面角.
(2)要求二面角的余弦,要先构造出二面角的平面角,然后利用解三角形的方法,求出这个平面角的余弦值,进而给出二面角的余弦值.
(3)线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.
法二,根据题意,构造空间直角坐标系,求出各点的坐标,进行求出相应直线的方向向量和平面的法向量,利用向量法进行求解(1)利用直线的方向向量与平面的法向量之间的关系,判断线面关系,
(2)通过求两个平面法向量的夹角求二面角.
解答: 解:法一:(I)如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
解:法一:(I)如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
又AB?平面DEF,EF?平面DEF.∴AB∥平面DEF.
(II)∵AD⊥CD,BD⊥CD∴∠ADB是二面角A-CD-B的平面角
∴AD⊥BD∴AD⊥平面BCD
取CD的中点M,这时EM∥AD∴EM⊥平面BCD
过M作MN⊥DF于点N,连接EN,则EN⊥DF
∴∠MNE是二面角E-DF-C的平面角
在Rt△EMN中,EM=1,MN=
∴tan∠MNE=
,cos∠MNE=y=-
x+2
.
(Ⅲ)在线段BC上存在点P,使AP⊥DE
证明如下:在线段BC上取点P.使BP=
BC,过P作PQ⊥CD与点Q,
∴PQ⊥平面ACD∵DQ=
DC=
在等边△ADE中,∠DAQ=30°
∴AQ⊥DE∴AP⊥DE.
法二:(Ⅱ)以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,
则A(0,0,2)B(2,0,0)C(0,2
,0,),E(0,
,1),F(1,
,0)
平面CDF的法向量为
=(0,0,2)设平面EDF的法向量为
=(x,y,z)
则
即
取
=(3,-
,3)cos<
,
>=
=
所以二面角E-DF-C的余弦值为
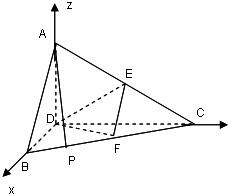 (Ⅲ)在平面坐标系xDy中,直线BC的方程为y=-
(Ⅲ)在平面坐标系xDy中,直线BC的方程为y=-
x+2
设P(x,2
-
x,0),则
=(x,2
-
x,-2)
∴AP⊥DE?
•
=0?x=
?
=
所以在线段BC上存在点P,使AP⊥DE
另解:设P(x,y,0),则
•
=
y-2=0∴y=
又
=(x-2,y,0),
=(-x,2
-y,0)
∵
∥
∴(x-2)(2
-y)=-xy∴
x+y=2
把y=
代入上式得x=
,
∴
=
所以在线段BC上存在点P使AP⊥DE
 解:法一:(I)如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,
解:法一:(I)如图:在△ABC中,由E、F分别是AC、BC中点,得EF∥AB,又AB?平面DEF,EF?平面DEF.∴AB∥平面DEF.
(II)∵AD⊥CD,BD⊥CD∴∠ADB是二面角A-CD-B的平面角
∴AD⊥BD∴AD⊥平面BCD
取CD的中点M,这时EM∥AD∴EM⊥平面BCD
过M作MN⊥DF于点N,连接EN,则EN⊥DF
∴∠MNE是二面角E-DF-C的平面角
在Rt△EMN中,EM=1,MN=
| ||
| 2 |
∴tan∠MNE=
| ||
| 2 |
| 3 |
| 3 |
(Ⅲ)在线段BC上存在点P,使AP⊥DE
证明如下:在线段BC上取点P.使BP=
| 1 |
| 3 |
∴PQ⊥平面ACD∵DQ=
| 1 |
| 3 |
2
| ||
| 3 |
∴AQ⊥DE∴AP⊥DE.
法二:(Ⅱ)以点D为坐标原点,直线DB、DC为x轴、y轴,建立空间直角坐标系,
则A(0,0,2)B(2,0,0)C(0,2
| 3 |
| 3 |
| 3 |
平面CDF的法向量为
| DA |
| n |
则
|
|
| n |
| 3 |
| DA |
| n |
| ||||
|
|
| ||
| 7 |
所以二面角E-DF-C的余弦值为
| ||
| 7 |
 (Ⅲ)在平面坐标系xDy中,直线BC的方程为y=-
(Ⅲ)在平面坐标系xDy中,直线BC的方程为y=-| 3 |
| 3 |
设P(x,2
| 3 |
| 3 |
| AP |
| 3 |
| 3 |
∴AP⊥DE?
| AP |
| DE |
| 4 |
| 3 |
| BP |
| 1 |
| 3 |
| BC |
所以在线段BC上存在点P,使AP⊥DE
另解:设P(x,y,0),则
| AP |
| DE |
| 3 |
2
| ||
| 3 |
又
| BP |
| PC |
| 3 |
∵
| BP |
| PC |
| 3 |
| 3 |
| 3 |
把y=
2
| ||
| 3 |
| 4 |
| 3 |
∴
| BP |
| 1 |
| 3 |
| BC |
点评:判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a?α,b?α,a∥b?a∥α);③利用面面平行的性质定理(α∥β,a?α?a∥β);④利用面面平行的性质(α∥β,a?α,a?,a∥α??a∥β).线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.本题也可以用空间向量来解决,其步骤是:建立空间直角坐标系?明确相关点的坐标?明确相关向量的坐标?通过空间向量的坐标运算求解.

练习册系列答案
相关题目