题目内容
【题目】已知函数f(x)=|x+a|(a>-2)的图象过点(2,1).
(1)求实数a的值;
(2)设![]() ,在如图所示的平面直角坐标系中作出函数y=g(x)的简图,并写出(不需要证明)函数g(x)的定义域、奇偶性、单调区间、值域.
,在如图所示的平面直角坐标系中作出函数y=g(x)的简图,并写出(不需要证明)函数g(x)的定义域、奇偶性、单调区间、值域.

【答案】(1)-1(2)详见解析
【解析】
(1)直接利用待定系数法求出a的值.
(2)利用(1)的结论求出函数g(x)的图象,进一步画出函数图象的简图,利用函数的图象确定函数的定义域,值域和单调区间.
(1)函数f(x)=|x+a|(a>-2)的图象过点(2,1).
则:1=|2+a|,解得:a=-1;
(2)设![]() ,
,
由于a=-1,则g(x)=![]() ,
,
定义域(-∞,1)∪(1,+∞),
由于g(-x)≠g(x)≠-g(x),所以函数为:非奇非偶函数.
g(x)=![]() =
=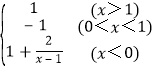 ,
,
函数的图象如下:

所以函数的值域:[-1,1];
函数单调递减区间为(-∞,0).

练习册系列答案
相关题目
