Question

【题目】已知函数f（x）=+lg（3x）的定义域为M．

（Ⅰ）求M；

（Ⅱ）当x∈M时，求g（x）=4x-2x+1+2的值域．

Answer 1

【答案】（Ⅰ）（-1，2]；（Ⅱ）[1，10].

【解析】

（Ⅰ）根据二次根式有意义条件，及对数函数真数大于0的条件，列出不等式，解不等式组即可得到定义域M。

（Ⅱ）将g（x）配方，化为关于2x的二次函数型函数，根据x的取值范围，即可得到函数的值域。

（Ⅰ）要使f（x）有意义，则，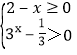

∴-1＜x≤2，

∴M=（-1，2]，

（Ⅱ）g（x）=4x-2x+1+2=（2x）2-22x+2=（2x-1）2+1；

∵x∈（-1，2]；

∴；

∴2x=1，即x=0时，g（x）min=1；

2x=4，即x=2时，g（x）max=10；

∴g（x）的值域为[1，10]．