题目内容
16.已知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1的左顶点为A、上顶点为B,光线通过点C(-1,0)射到线段AB(端点除外)上的点T,经线段AB反射,其反射光线与椭圆交于点M.若∠CTM为钝角,则T点的横坐标m的范围为(-3,$\frac{-3-\sqrt{3}}{2}$)∪($\frac{\sqrt{3}-3}{2}$,0).分析 只要求出∠CTM为直角时T的横坐标.由图可得,这样的T点有两个.求出A,B,|AB|的长,可得∠BAC=30°,运用解直角三角形的知识,结合反射定律,可得T的横坐标,再由图形观察,即可得到范围.
解答 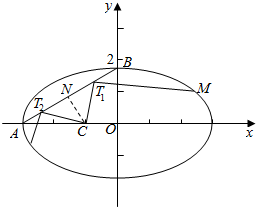 解:只要求出∠CTM为直角时T的横坐标.
解:只要求出∠CTM为直角时T的横坐标.
由图可得,这样的T点有两个.
先求线段AB上面的一个,设为T1,
A(-3,0),B(0,$\sqrt{3}$),|AB|=$\sqrt{9+3}$=2$\sqrt{3}$,
即有∠BAC=30°,
又|AC|=2,可得C到AB的距离CN为1,
由∠CT1M为直角,由反射定律可得,∠AT1C=45°,
AN=$\sqrt{4-1}$=$\sqrt{3}$,T1N=1,即有AT1=1+$\sqrt{3}$,
T1的横坐标即为$\frac{\sqrt{3}}{2}$(1+$\sqrt{3}$)-3=$\frac{\sqrt{3}-3}{2}$,
同理可得AT2=$\sqrt{3}$-1,
T2的横坐标为$\frac{-3-\sqrt{3}}{2}$,
由图象观察可得,若∠CTM为钝角,
则T点的横坐标m的范围是(-3,为$\frac{-3-\sqrt{3}}{2}$)∪($\frac{\sqrt{3}-3}{2}$,0).
故答案为:(-3,$\frac{-3-\sqrt{3}}{2}$)∪($\frac{\sqrt{3}-3}{2}$,0).
点评 本题考查椭圆的方程和性质,考查光线反射定律的运用,同时考查转化思想的运用,以及数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
6.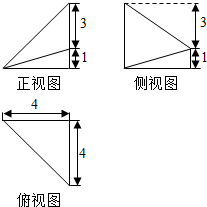 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )
 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{40}{3}$ | D. | .20 |
6.已知D,E,F分别是△ABC三边AB,BC,CA的中点,则下列等式不成立的是( )
| A. | $\overrightarrow{FD}$+$\overrightarrow{DA}$=$\overrightarrow{FA}$ | B. | $\overrightarrow{FD}$+$\overrightarrow{DE}$+$\overrightarrow{EF}$=0 | C. | $\overrightarrow{DE}$+$\overrightarrow{DA}$=$\overrightarrow{EC}$ | D. | $\overrightarrow{DA}$+$\overrightarrow{DE}$=$\overrightarrow{DF}$ |
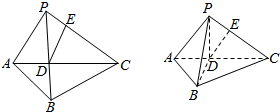 如图,在四边形PABC中,PB⊥AC,AD=BD=1,AC=3,E是PC上一点,且PE:EC=1:2,现将△PAC沿AC进行翻折,得到如图②所示的三棱锥P-ABC.
如图,在四边形PABC中,PB⊥AC,AD=BD=1,AC=3,E是PC上一点,且PE:EC=1:2,现将△PAC沿AC进行翻折,得到如图②所示的三棱锥P-ABC.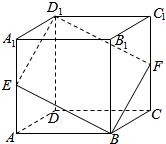
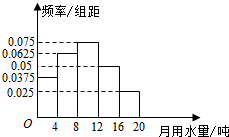 为提倡市民节约用水,中国水利部确定每年的3月22日至28日为“中国水周”,某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.
为提倡市民节约用水,中国水利部确定每年的3月22日至28日为“中国水周”,某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.