题目内容
【题目】已知函数f(x)=x3-3x2+1,g(x)= ,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
,若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是______.
【答案】![]()
【解析】分析:利用换元法设t=f(x),则g(t)=a分别作出两个函数的图象,根据a的取值确定t的取值范围,利用数形结合进行求解判断即可.
详解:作出函数f(x)和g(x)的图象如图: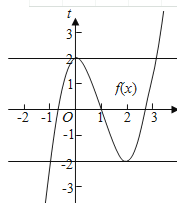 ,
,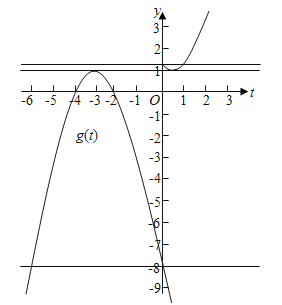 ,由g[f(x)]-a=0(a>0)得g[f(x)]=a,(a>0)设t=f(x),则g(t)=a,(a>0)由y=g(t)的图象知,①当0<a<1时,方程g(t)=a有两个根-4<t1<-3,或-4<t2<-2,由t=f(x)的图象知,当-4<t1<-3时,t=f(x)有0个根,当-4<t2<-2时,t=f(x)有0个根,此时方程g[f(x)]-a=0(a>0)有0个根,②当a=1时,方程g(t)=a有两个根t1=-3,或t2=
,由g[f(x)]-a=0(a>0)得g[f(x)]=a,(a>0)设t=f(x),则g(t)=a,(a>0)由y=g(t)的图象知,①当0<a<1时,方程g(t)=a有两个根-4<t1<-3,或-4<t2<-2,由t=f(x)的图象知,当-4<t1<-3时,t=f(x)有0个根,当-4<t2<-2时,t=f(x)有0个根,此时方程g[f(x)]-a=0(a>0)有0个根,②当a=1时,方程g(t)=a有两个根t1=-3,或t2=![]() ,由t=f(x)的图象知,当t1=-3时,t=f(x)有0个根,当t2=
,由t=f(x)的图象知,当t1=-3时,t=f(x)有0个根,当t2=![]() 时,t=f(x)有3个根,此时方程g[f(x)]-a=0(a>0)有3个根,③当1<a<
时,t=f(x)有3个根,此时方程g[f(x)]-a=0(a>0)有3个根,③当1<a<![]() 时,方程g(t)=a有两个根0<t1<
时,方程g(t)=a有两个根0<t1<![]() ,或
,或![]() <t2<1,由t=f(x)的图象知,当0<t1<
<t2<1,由t=f(x)的图象知,当0<t1<![]() 时,t=f(x)有3个根,当
时,t=f(x)有3个根,当![]() <t2<1时,t=f(x)有3个根,此时方程g[f(x)]-a=0(a>0)有3+3=6个根,当a=
<t2<1时,t=f(x)有3个根,此时方程g[f(x)]-a=0(a>0)有3+3=6个根,当a=![]() 由图可得同理只有5解,综合的故若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是
由图可得同理只有5解,综合的故若方程g[f(x)]-a=0(a>0)有6个实数根(互不相同),则实数a的取值范围是![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?