题目内容
在直角坐标系中,曲线 的参数方程为
的参数方程为 ,以
,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 在极坐标系中的方程为
在极坐标系中的方程为 .若曲线
.若曲线 与
与 有两个不同的交点,则实数
有两个不同的交点,则实数 的取值范围是 .
的取值范围是 .
 的参数方程为
的参数方程为 ,以
,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 在极坐标系中的方程为
在极坐标系中的方程为 .若曲线
.若曲线 与
与 有两个不同的交点,则实数
有两个不同的交点,则实数 的取值范围是 .
的取值范围是 . 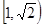
试题分析:因为曲线
 的参数方程为
的参数方程为 化成直角坐标方程为: x2+y2=1,图象是圆心在原点半径为1的上半圆.曲线C2利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程,在直角坐标方程方程是: x-y+b=0.由圆心到直线的距离得:d=
化成直角坐标方程为: x2+y2=1,图象是圆心在原点半径为1的上半圆.曲线C2利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程,在直角坐标方程方程是: x-y+b=0.由圆心到直线的距离得:d=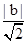 =1,得到b=±
=1,得到b=±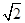
结合图象得:实数b的取值范围是1≤b<
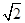
故答案为:1≤b<
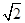
点评:解决该试题的关键是先消去参数θ得到曲线的普通方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得曲线C2在的直角坐标方程.在直角坐标系中画出它们的图形,由图观察即可得实数b的取值范围。

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
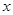 轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点
轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点 为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线
为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线 对称.
对称. 与双曲线C的左支交于A,B两点,另一直线
与双曲线C的左支交于A,B两点,另一直线 经过M(-2,0)及AB的中点,求直线
经过M(-2,0)及AB的中点,求直线 轴上的截距b的取值范围.
轴上的截距b的取值范围.  的长轴
的长轴 分成
分成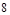 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于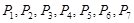 七个点,
七个点, 是椭圆的一个焦点,则
是椭圆的一个焦点,则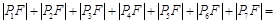 ( )
( )
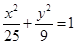 上一点
上一点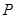 到一个焦点的距离为5,则
到一个焦点的距离为5,则 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且
为椭圆上一点,且 ,则
,则 的面积为
的面积为


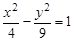 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为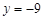 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截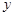 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线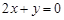 上,并与
上,并与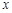 轴相切,求该圆的方程.
轴相切,求该圆的方程. 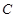 :
: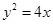 的焦点为
的焦点为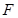 ,直线
,直线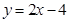 与
与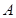 、
、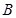 两点.则
两点.则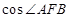 ="________."
="________." 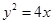 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点,点
两点,点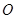 是原点,若
是原点,若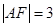 ,则
,则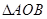 的面积为
的面积为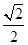



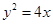 上一点
上一点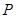 引其准线的垂线,垂足为
引其准线的垂线,垂足为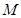 ,设抛物线的焦点为
,设抛物线的焦点为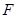 ,且
,且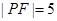 ,则
,则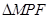 的面积为 .
的面积为 .