题目内容
【题目】已知椭圆![]() :
: ![]() ,左焦点是
,左焦点是![]() .
.
(1)若左焦点![]() 与椭圆
与椭圆![]() 的短轴的两个端点是正三角形的三个顶点,点
的短轴的两个端点是正三角形的三个顶点,点![]() 在椭圆
在椭圆![]() 上.求椭圆
上.求椭圆![]() 的方程;
的方程;
(2)过原点且斜率为![]() 的直线
的直线![]() 与(1)中的椭圆
与(1)中的椭圆![]() 交于不同的两点
交于不同的两点![]() ,设
,设![]() ,求四边形
,求四边形![]() 的面积取得最大值时直线
的面积取得最大值时直线![]() 的方程;
的方程;
(3)过左焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,其中
,其中![]() 是常数,设
是常数,设![]() ,
, ![]() ,计算
,计算![]() 的值(用
的值(用![]() 的代数式表示).
的代数式表示).
【答案】(1)![]() (2)
(2)![]() (3)
(3)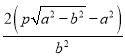
【解析】试题分析:(1)利用已知条件列方程组求出![]() 的值,从而求出椭圆的标准方程; (2)设直线
的值,从而求出椭圆的标准方程; (2)设直线![]() 的方程
的方程![]() ,联立直线
,联立直线![]() 和椭圆方程,求出
和椭圆方程,求出![]() ,分别求出点
,分别求出点![]() 到直线
到直线![]() 的距离,求出四边形
的距离,求出四边形![]() 的面积,利用基本不等式求出最大值得到
的面积,利用基本不等式求出最大值得到![]() ,再求出直线
,再求出直线![]() 的方程; (3)设直线
的方程; (3)设直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 和椭圆方程,求出两根之和,两根之积, 由向量共线求出
和椭圆方程,求出两根之和,两根之积, 由向量共线求出![]() 的表达式,代入化简,求出
的表达式,代入化简,求出![]() 的值.
的值.
试题解析:(1)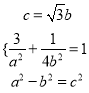
![]() , 所以椭圆方程
, 所以椭圆方程![]()
(2)设直线![]() 的方程
的方程![]()
联立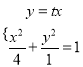 ,可以计算
,可以计算![]()
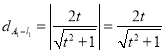 ,
, ![]()
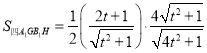
![]()
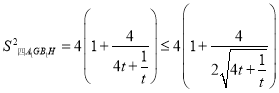
![]() 所以直线
所以直线![]() 的方程是
的方程是![]()
(3)设直线![]() 的方程
的方程![]() 交椭圆
交椭圆![]() 于
于![]()
![]()
![]()
直线![]() 交直线
交直线![]() 于点
于点![]() ,根据题设
,根据题设![]() ,
, ![]() 得到
得到
![]() ,
, ![]() ,
,
得![]() ,
, ![]()
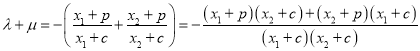
![]()
![]()
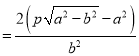
点睛: 本题主要考查了求椭圆的方程, 四边形面积的计算, 以及求参数![]() 的值, 属于中档题. 本题涉及的考点有椭圆标准方程,点到直线距离公式,基本不等式,向量共线定理等,考查学生的运算求解能力以及分析问题、解决问题的能力.
的值, 属于中档题. 本题涉及的考点有椭圆标准方程,点到直线距离公式,基本不等式,向量共线定理等,考查学生的运算求解能力以及分析问题、解决问题的能力.

练习册系列答案
相关题目