题目内容
设函数y=f(x)是定义在R+上的函数,并且满足下面三个条件:(1)对任意正数x、y,都有f(xy)=f(x)+f(y);
(2)当x>1时,f(x)<0;
(3)f(3)=-1,
(I)求f(1)、
 的值;
的值;(II)如果不等式f(x)+f(2-x)<2成立,求x的取值范围.
(III)如果存在正数k,使不等式f(kx)+f(2-x)<2有解,求正数k的取值范围.
【答案】分析:(I)对于任意的x,y∈(0,+∞),f(x•y)=f(x)+f(y),令x=y=1,x=y=3,即可求得f(1)、 的值;且当x>1时,f(x)<0,根据函数单调性的定义讨论函数的单调性.
的值;且当x>1时,f(x)<0,根据函数单调性的定义讨论函数的单调性.
(II)f(x)+f(2-x)=f[x(2-x)],根据函数的单调性把函数值不等式转化为自变量不等式,解不等式即可求得结果.
(III)把f(kx)+f(2-x)根据条件转化为f[kx(2-x)],根据函数的单调性把函数值不等式转化为自变量不等式有解,分离参数转化我求函数的最值问题.
解答:解:(I)令x=y=1易得f(1)=0.
而f(9)=f(3)+f(3)=-1-1=-2 且 ,
,
得 .
.
(II)设0<x1<x2<+∞,由条件(1)可得 ,
,
因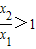 ,由(2)知
,由(2)知 ,
,
所以f(x2)<f(x1),
即f(x)在R+上是递减的函数.
由条件(1)及(I)的结果得:
其中0<x<2,由函数f(x)在R+上的递减性,可得: ,
,
由此解得x的范围是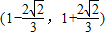 .
.
(III)同上理,不等式f(kx)+f(2-x)<2可化为 且0<x<2,
且0<x<2,
得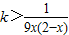 ,此不等式有解,等价于
,此不等式有解,等价于 ,
,
在0<x<2的范围内,易知x(2-x)max=1,
故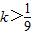 即为所求范围.
即为所求范围.
点评:考查利用函数单调性的定义探讨抽象函数的单调性问题,对于解决抽象函数的一般采用赋值法,求某些点的函数值和证明不等式等,体现了转化的思想,(III)不等式f(kx)+f(2-x)<2有解,采取分离参数的方法,转化为函数的最值问题,加大了试题的难度,属中档题.
 的值;且当x>1时,f(x)<0,根据函数单调性的定义讨论函数的单调性.
的值;且当x>1时,f(x)<0,根据函数单调性的定义讨论函数的单调性.(II)f(x)+f(2-x)=f[x(2-x)],根据函数的单调性把函数值不等式转化为自变量不等式,解不等式即可求得结果.
(III)把f(kx)+f(2-x)根据条件转化为f[kx(2-x)],根据函数的单调性把函数值不等式转化为自变量不等式有解,分离参数转化我求函数的最值问题.
解答:解:(I)令x=y=1易得f(1)=0.
而f(9)=f(3)+f(3)=-1-1=-2 且
 ,
,得
 .
.(II)设0<x1<x2<+∞,由条件(1)可得
 ,
,因
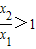 ,由(2)知
,由(2)知 ,
,所以f(x2)<f(x1),
即f(x)在R+上是递减的函数.
由条件(1)及(I)的结果得:

其中0<x<2,由函数f(x)在R+上的递减性,可得:
 ,
,由此解得x的范围是
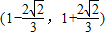 .
.(III)同上理,不等式f(kx)+f(2-x)<2可化为
 且0<x<2,
且0<x<2,得
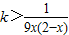 ,此不等式有解,等价于
,此不等式有解,等价于 ,
,在0<x<2的范围内,易知x(2-x)max=1,
故
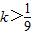 即为所求范围.
即为所求范围.点评:考查利用函数单调性的定义探讨抽象函数的单调性问题,对于解决抽象函数的一般采用赋值法,求某些点的函数值和证明不等式等,体现了转化的思想,(III)不等式f(kx)+f(2-x)<2有解,采取分离参数的方法,转化为函数的最值问题,加大了试题的难度,属中档题.

练习册系列答案
相关题目