题目内容
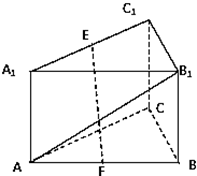 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=a,E是A1C1的中点,F是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=a,E是A1C1的中点,F是AB中点.(1)求证:EF∥面BB1C1C;
(2)求直线EF与直线CC1所成角的正切值.
分析:(1)利用线面平行的判定定理,证明平面EFG∥平面BB1C1C,即可.
(2)根据直线所成角的定义,进行求解.
(2)根据直线所成角的定义,进行求解.
解答:解:(1)取AC的中点G,连结EG,FG,
∵EG∥C1C,C1C?平面EFG,
∴C1C∥平面EFG,
同理可证BC∥平面EFG,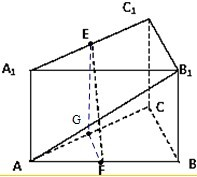
又∵BC,C1C?面BB1C1C,
∴平面EFG∥平面BB1C1C,
∴EF∥面BB1C1C.
(2)∵在三棱柱ABC-A1B1C1中,∴EG⊥面BB1C1C,
∵EG∥C1C,
∴∠FEG为直线EF与C1C所成的角,
∵△EFG为直角三角形,
∴tan∠EFG=
=
=
.
∵EG∥C1C,C1C?平面EFG,
∴C1C∥平面EFG,
同理可证BC∥平面EFG,

又∵BC,C1C?面BB1C1C,
∴平面EFG∥平面BB1C1C,
∴EF∥面BB1C1C.
(2)∵在三棱柱ABC-A1B1C1中,∴EG⊥面BB1C1C,
∵EG∥C1C,
∴∠FEG为直线EF与C1C所成的角,
∵△EFG为直角三角形,
∴tan∠EFG=
| FG |
| EG |
| ||
| a |
| 1 |
| 2 |
点评:本题主要考查线面平行的判定以及直线所成角的定义及求法,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目




