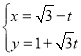题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() (
(![]() 为坐标原点)的面积为
为坐标原点)的面积为![]() .
.
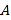
(1)求椭圆![]() 的方程;
的方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点)
为椭圆上一动点(非长轴端点)![]() ,
,![]() 为左、右焦点,
为左、右焦点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意求得a,b,c的值即可确定椭圆方程;
(2)分类讨论直线的斜率存在和斜率不存在两种情况,联立直线方程与椭圆方程,结合韦达定理和均值不等式即可确定三角形面积的最大值.
(1)椭圆![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,
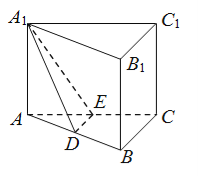
可设![]() ,
,![]() ,
,
∵![]() 的面积为
的面积为![]() ,
,
∴![]() ,解得
,解得![]() ,∴
,∴![]() ,
,![]() ,
,
由已知得 ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,不妨取
的斜率不存在时,不妨取![]() ,
,![]() ,
,![]() ,故
,故
![]() ;
;
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
联立方程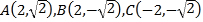 ,化简得
,化简得![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
![]()
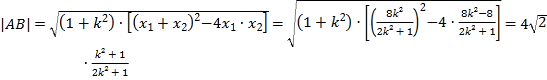
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
因为![]() 是线段
是线段![]() 的中点,所以点
的中点,所以点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]()
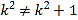
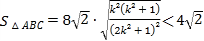
∵
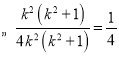 ,又
,又![]() ,所以等号不成立.
,所以等号不成立.
∴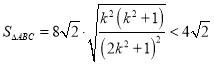 ,
,
综上,![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】古人云:“腹有诗书气自华.”为响应全民阅读,建设书香中国,校园读书活动的热潮正在兴起.某校为统计学生一周课外读书的时间,从全校学生中随机抽取![]() 名学生进行问卷调査,统计了他们一周课外读书时间(单位:
名学生进行问卷调査,统计了他们一周课外读书时间(单位:![]() )的数据如下:
)的数据如下:
一周课外读书时间/ |
|
|
|
|
|
|
|
|
| 合计 |
频数 | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
频率 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
(1)根据表格中提供的数据,求![]() ,
,![]() ,
,![]() 的值并估算一周课外读书时间的中位数.
的值并估算一周课外读书时间的中位数.
(2)如果读书时间按![]() ,
,![]() ,
,![]() 分组,用分层抽样的方法从
分组,用分层抽样的方法从![]() 名学生中抽取20人.
名学生中抽取20人.
①求每层应抽取的人数;
②若从![]() ,
,![]() 中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
中抽出的学生中再随机选取2人,求这2人不在同一层的概率.