题目内容
正三棱锥S─ABC内接于球O,其底面边长是2
,侧棱长是4,则球O的体积是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:判断球心的位置,利用已知条件求出球的半径,即可求解球的体积.
解答: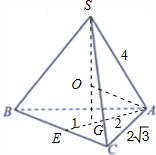 解:画出正三棱锥S─ABC的图形,由题意可知,球心O在正三棱锥的高上,
解:画出正三棱锥S─ABC的图形,由题意可知,球心O在正三棱锥的高上,
如图,则OS=OA=OB=OC=R,
底面边长是2
,∴GA=
×
×2
=2,
∵侧棱长是4,
∴SG=
=2
.
在三角形OAG中,OA=
,
可得R2=(2
-R)2+22,
解得R=
.
球O的体积是:
πR3=
π(
)3=
.
故选:D.
 解:画出正三棱锥S─ABC的图形,由题意可知,球心O在正三棱锥的高上,
解:画出正三棱锥S─ABC的图形,由题意可知,球心O在正三棱锥的高上,如图,则OS=OA=OB=OC=R,
底面边长是2
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
∵侧棱长是4,
∴SG=
| 42-22 |
| 3 |
在三角形OAG中,OA=
| AG2+OG2 |
可得R2=(2
| 3 |
解得R=
4
| ||
| 3 |
球O的体积是:
| 4 |
| 3 |
| 4 |
| 3 |
4
| ||
| 3 |
256
| ||
| 27 |
故选:D.
点评:本题考查球与多面体的关系,球的体积的求法,正确处理二者的关系是解题的关键,考查空间想象能力以及计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
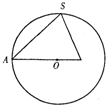 已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为