题目内容
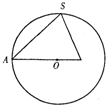已知正三棱锥S-ABC内接于半径为6的球，过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图，则此三棱锥的侧面积为27
| 15 |
27
．| 15 |
分析：根据图示，这个截面三角形图由原正三棱锥的一条棱，一个侧面三角形的中线和底面正三角形的中线围成，正三棱锥的外接球的球心在底面正三角形的重心上，从而可求得侧面的底边长与高，故可求．
解答：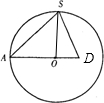
解：根据图示，这个截面三角形图由原正三棱锥的一条棱，一个侧面三角形的中线和底面正三角形的中线围成，正三棱锥的外接球的球心在底面正三角形的重心上，于是有半径R=
底面中线长
设BC的中点为D，连接SO
∵R=6
∴AD=9，
∴OD=3，SD=
=
，BC=6
，
∴三棱锥的侧面积=3×
×
×6
=27
．
故答案为：27
解：根据图示，这个截面三角形图由原正三棱锥的一条棱，一个侧面三角形的中线和底面正三角形的中线围成，正三棱锥的外接球的球心在底面正三角形的重心上，于是有半径R=| 2 |
| 3 |
设BC的中点为D，连接SO
∵R=6
∴AD=9，
∴OD=3，SD=
| 62+32 |
| 45 |
| 3 |
∴三棱锥的侧面积=3×
| 1 |
| 2 |
| 45 |
| 3 |
| 15 |
故答案为：27
| 15 |
点评：本题考查空间想象能力，关键是要抓住这个截面三角形图由原正三棱锥的一条棱，一个侧面三角形的中线和底面正三角形的中线围成，正三棱锥的外接球的球心在底面正三角形的重心上．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
