题目内容
正三棱锥S-ABC内接于球O,且球心O在平面ABC上,若正三棱锥S-ABC的底面边长为a,则该三棱锥的体积是
a3
a3.
| 1 |
| 12 |
| 1 |
| 12 |
分析:由题意求出底面面积及三棱锥S-ABC的高,然后求出三棱锥的体积.
解答: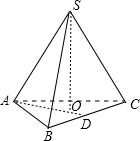 解:三棱锥S-ABC中,PO⊥底面ABC,
解:三棱锥S-ABC中,PO⊥底面ABC,
底面ABC是边长为a的正三角形,所以底面面积为:
a 2;
在三角形ABC中,O是其中心,故AO=
AD=
×
a=
a
即三棱锥S-ABC的高SO=AO=
a
三棱锥的体积为:
×
a 2×
a=
a3
故答案为:
a3.
 解:三棱锥S-ABC中,PO⊥底面ABC,
解:三棱锥S-ABC中,PO⊥底面ABC,底面ABC是边长为a的正三角形,所以底面面积为:
| ||
| 4 |
在三角形ABC中,O是其中心,故AO=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
即三棱锥S-ABC的高SO=AO=
| ||
| 3 |
三棱锥的体积为:
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 1 |
| 12 |
故答案为:
| 1 |
| 12 |
点评:本题是基础题,考查球内接多面体、三棱锥的体积的计算,注意三棱锥的特征是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
正三棱锥S─ABC内接于球O,其底面边长是2
,侧棱长是4,则球O的体积是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
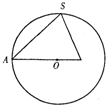 已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为