题目内容
【题目】已知函数![]() =
= ![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的值,并判断
的值,并判断![]() 在
在![]() 处取得极大值还是极小值.
处取得极大值还是极小值.
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由![]() 得到
得到![]() ,并通过求导判断得到
,并通过求导判断得到![]() 处取得极小值;(2)
处取得极小值;(2)![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,通过分类讨论,得到
,通过分类讨论,得到![]() 时,
时, 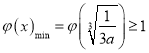 ,所以
,所以![]() 。
。
试题解析:
(1)![]() 的定义域是
的定义域是![]() ,
,![]() =
=![]() ,由
,由![]() 得
得![]() .
.
当![]() 时,
时,![]() =
=![]() ,
,![]() =
=![]()
![]()
![]()
![]() 恒成立,
恒成立,![]() 令
令![]() =
=![]() ,
,![]() =
=![]()
![]() 恒成立
恒成立
![]()
![]() 在
在![]() 上单调递增,又因为
上单调递增,又因为![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
![]() 当
当![]() 时,
时,![]() 在
在![]() 处取得极小值.
处取得极小值.
(2)由![]() 得
得![]() 在
在![]() 上恒成立
上恒成立
即![]() 在
在![]() 上恒成立.
上恒成立.
解法一(将绝对值看成一个函数的整体进行研究):
令![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() ,所以
,所以![]() 的值域为:
的值域为:![]() ,因为
,因为![]() ,所以
,所以![]() 的值域为
的值域为![]() ;所以不成立.
;所以不成立.
②当![]() 时,易知
时,易知![]() 恒成立.
恒成立.![]() ,所以
,所以![]() 在
在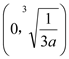 上单调递减,在
上单调递减,在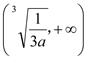 上单调递增.因为
上单调递增.因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在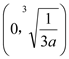 上单调递减,在
上单调递减,在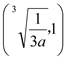 上单调递增.所以
上单调递增.所以![]()
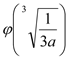 ,依题意,
,依题意,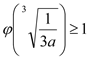 ,所以
,所以![]() .
.
综上:![]()
解法二(求命题的否定所对应的集合,再求该集合的补集):
命题“![]() 对
对![]() 都成立”的否定是“
都成立”的否定是“![]() 在
在![]() 上有解”
上有解”
![]() 在
在![]() 上有解
上有解![]()
![]() 在
在![]() 上有解
上有解
![]()
![]() 在
在![]() 上有解
上有解
令![]() ,
,![]() .
.
![]()
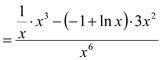
![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]()
![]() ,所以
,所以![]() 无最小值.所以
无最小值.所以![]() ;
;
令![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() ,所以
,所以![]() .
.
因为![]() 在
在![]() 上有解时,
上有解时,![]() ;
;
所以![]() 对
对![]() 都成立时,
都成立时,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目