题目内容
5. 如图,在三棱柱ABC-A1B1C1中,已知 AB=BC=1,CC1=2,AC1与平面 BCC1B1所成角为30°,AB⊥平面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知 AB=BC=1,CC1=2,AC1与平面 BCC1B1所成角为30°,AB⊥平面BB1C1C.(Ⅰ)求证:BC⊥AC1;
(Ⅱ)求三棱锥A-A1B1C1的高.
分析 (Ⅰ)连接BC1,从而可得∠AC1B=30°,且$B{C^2}+B{C_1}^2=C{C_1}^2$,从而可证明CB⊥平面ABC1,从而证明;
(Ⅱ)由三棱锥与三棱柱的关系知,${V_{A-{A_1}{B_1}{C_1}}}={V_{A-B{C_1}{B_1}}}=\frac{1}{3}AB•{S_{△B{C_1}{B_1}}}=\frac{{\sqrt{3}}}{6}$,且${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}$×1×1=$\frac{1}{2}$;从而求高.
解答 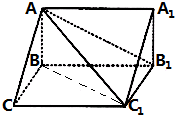 解:(Ⅰ)证明:连接BC1,
解:(Ⅰ)证明:连接BC1,
∵AB⊥平面BCC1B1,
∴∠AC1B=30°.
∵AB=1,
∴$B{C_1}=\sqrt{3}$;
∵BC=1,CC1=2,
∴$B{C^2}+B{C_1}^2=C{C_1}^2$,
即∠CBC1=90°.
∵CB⊥AB,CB⊥BC1,
∴CB⊥平面ABC1,
∴BC⊥AC1;
(Ⅱ)解:∵${V_{A-{A_1}{B_1}{C_1}}}={V_{A-B{C_1}{B_1}}}=\frac{1}{3}AB•{S_{△B{C_1}{B_1}}}=\frac{{\sqrt{3}}}{6}$,
${S}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}$×1×1=$\frac{1}{2}$;
∴三棱锥A-A1B1C1的高H=$\sqrt{3}$.
点评 本题考查了学生的空间想象力与作图能力的运用,同时考查了体积的运算与应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知z1=2+i,z2=1-2i,则复数z=z2-z1对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在棱长为a的正方体A1B1C1D1-ABCD中,
如图,在棱长为a的正方体A1B1C1D1-ABCD中, 如图,已知四边形AA1C1C和AA1B1B都是菱形,平面AA1B1B和平面AA1C1C互相垂直,且∠ACC1=∠BAA1=60°,AA1=2
如图,已知四边形AA1C1C和AA1B1B都是菱形,平面AA1B1B和平面AA1C1C互相垂直,且∠ACC1=∠BAA1=60°,AA1=2