题目内容
【题目】函数f（x）=x3+bx2+cx+d的图象如图，则函数g（x）=log 
（x2+ 
bx+ 
）的单调递增区间为（ ） 
A.[﹣2，+∞）
B.（﹣∞，﹣2）
C.（3，+∞）
D.[3，+∞）
【答案】B
【解析】解：由图象得函数过原点，则f（0）=d=0，
函数的导数f′（x）=3x2+2bx+c，
x=﹣2和x=3是函数f（x）的极值点，
则x=﹣2和x=3是方程f′（x）=3x2+2bx+c=0的两个根，
则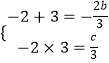 
，即b=﹣ 
，c=﹣18，
则g（x）=log 
（x2+ 
bx+ 
）=log （x2﹣x﹣6），
设t=x2﹣x﹣6，则函数y=log t为减函数，
由t=x2﹣x﹣6＞0得x＞3或x＜﹣2，
要求g（x）的单调递增区间，即求函数t=x2﹣x﹣6的单调递减区间，
∵t=x2﹣x﹣6的单调递减区间为（﹣∞，﹣2），
∴函数g（x）=log （x2+ bx+ ）的单调递增区间为（﹣∞，﹣2），
故选：B
练习册系列答案
相关题目
