题目内容
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[100,110),[110,120),[120,130)三组内的学生中,用分层抽样的方法选取28人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为 . 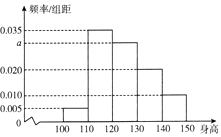
【答案】12
【解析】解:由频率分布直方图,得身高在[120,130)内的频率为: 1﹣(0.005+0.010+0.020+0.035)×10=0.3,
所以身高在[100,110),[110,120),[120,130)三组频率分别为0.05,0.35,0.3,
故三组的人数比为1:7:6;
∴用分层抽样的方法从三组选取28人参加一项活动,
从身高在[120,130)内的学生中抽取的人数应为:
28× ![]() =12.
=12.
所以答案是:12.
【考点精析】掌握频率分布直方图是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】甲、乙两人玩一种游戏,游戏规则如下:先将筹码放在如下表的正中间D处,投掷一枚质地均匀的硬币,若正面朝上,筹码向右移动一格;若反面朝上,筹码向左移动一格.
A | B | C | D | E | F | G |
30 | 5 | 10 | 10 | 5 | 20 | 30 |
(1)将硬币连续投掷三次,现约定:若筹码停在A或B或C或D处,则甲赢;否则,乙赢.问该约定对乙公平吗?请说明理由.
(2)设甲、乙两人各有100个积分,筹码停在D处,现约定: ①投掷一次硬币,甲付给乙10个积分;乙付给甲的积分数是,按照上述游戏规则筹码所在表中字母A﹣G下方所对应的数目;
②每次游戏筹码都连续走三步,之后重新回到起始位置D处.
你认为该规定对甲、乙二人哪一个有利,请说明理由.
【题目】某校开设的校本课程分别有人文科学、自然科学、艺术体育三个课程类别,每种课程类别开设课程数及学分设定如下表所示:
人文科学类 | 自然科学类 | 艺术体育类 | |
课程门数 | 4 | 4 | 2 |
每门课程学分 | 2 | 3 | 1 |
学校要求学生在高中三年内从中选修3门课程,假设学生选修每门课程的机会均等.
(Ⅰ)甲至少选1门艺术体育类课程,同时乙至多选1门自然科学类课程的概率为多少?
(Ⅱ)求甲选的3门课程正好是7学分的概率;
(Ⅲ)设甲所选3门课程的学分数为X,写出X的分布列,并求出X的数学期望.
【题目】交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 | A1 | A2 | A3 | A4 | A5 | A6 |
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950.记X为某同学家的一辆该品牌车在第四年续保时的费用,求X的分布列与数学期望值;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.

