题目内容
【题目】已知椭圆
的长轴长与焦距分别为方程
的两个实数根.
（1）求椭圆的标准方程；
（2）若直线
过点
且与椭圆相交于
，
两点，
是椭圆的左焦点，当
面积最大时，求直线的斜率.
【答案】（1）
；（2）
.
【解析】
（1）设椭圆的焦距为
，解方程
，可求出
、
的值，进而求出
的值，由此可得出椭圆的标准方程；
（2）设直线
的方程为
，设点
、
，将直线的方程与椭圆的标准方程联立，列出韦达定理，求出
的面积关于
的表达式，换元
，利用基本不等式求出面积的最大值，利用等号成立的条件求出的值，即可得出直线的斜率.
（1）设椭圆的焦距为，由可得
，
，
所以
，
，即
，
.所以
，
故椭圆的标准方程为；
（2）设直线的方程为，设、，
与椭圆方程联立得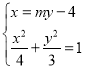
，消去
得
.
则
，所以
.
由根与系数的关系知
，
，
所以
.①
令，则①式可化为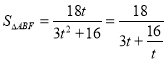
.
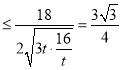当且仅当
，即
时，等号成立.
此时
，所以直线的斜率为.
【题目】如图，将边长为1的正方形ABCD沿x轴正向滚动，先以A为中心顺时针旋转，当B落在x轴时，又以B为中心顺时针旋转，如此下去，设顶点C滚动时的曲线方程为
，则下列说法不正确的是
A.
恒成立B.
C.
D.
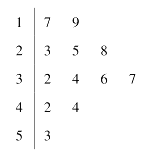
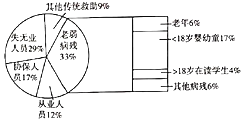
【题目】下表列出了10名5至8岁儿童的体重x(单位kg)(这是容易测得的)和体积y(单位dm3)(这是难以测得的)，绘制散点图发现，可用线性回归模型拟合y与x的关系：
体重x | 17.00 10.50 13.80 15.70 11.90 10.20 15.00 17.80 16.00 12.10 |
体积y | 16. 70 10.40 13.50 15.70 11.60 10.00 14.50 17.50 15.40 11.70 |
(1)求y关于x的线性回归方程
(系数精确到0.01)；
(2)某5岁儿童的体重为13.00kg，估测此儿童的体积．
附注：参考数据：
，
，
，
，
，
，137×14=1918.00．
参考公式：回归方程中斜率和截距的最小二乘法估计公式分别为：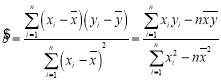
，
．
