题目内容
【题目】给出下列五个结论：
①在△ABC中，若sinA＞sinB，则必有cosA＜cosB；
②在△ABC中，若a，b，c成等比数列，则角B的取值范围为 
；
③等比数列{an}中，若a3=2，a7=8，则a5=±4；
④等差数列{an}的前n项和为Sn ， S10＜0且S11=0，满足Sn≥Sk对n∈N*恒成立，则正整数k构成集合为{5，6}
⑤若关于x的不等式（a2﹣1）x2﹣（a﹣1）x﹣1＜0的解集为R，则a的取值范围为 
．
其中正确结论的序号是 ． （填上所有正确结论的序号）．
【答案】①②④
【解析】解：①在△abc中，sinA＞sinB，根据正弦定理，根据大边对大角可得A＞B，根据余弦的图象，可得cosA＜cosB，所以正确；
②根据已知得：b2=ac，由余弦定理可得cosB= 
= 
≥ 
= 
，可得B∈ 
，所以正确；
③由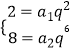 
，解得a1=1，q2=2，可得：a5= 
=4，所以不正确；
④解：∵Sn是等差数列{an}的前n项和，S10＜0，且S11=0，
∴ 
，即 
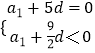④，
∴d＞0，a6=a1+5d=0，
∴a1到a5都是负数，a6是0，以后各项全是正数．
∵Sn≥Sk对n∈N+恒成立，∴k=5，或k=6．
∴正整数k构成的集合为{5，6}．故正确；
⑤解：设函数f（x）=（a2﹣1）x2﹣（a﹣1）x﹣1．由题设条件关于x的不等式（a2﹣1）x2﹣（a﹣1）x﹣1＜0的解集为R．
可得对任意的x属于R．都有f（x）＜0．
又当a≠1时，函数f（x）是关于x的抛物线．故抛物线必开口向下，且于x轴无交点．
故满足 
故解得﹣ 
＜x＜1．
当a=1时．f（x）=﹣1．成立．
综上，a的取值范围为（﹣ ，1]．
故不正确．所以答案是：①②④．
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能正确解答此题．
