题目内容
已知两定点 ,
, 为动点
为动点
(1)若 在x轴上方,且
在x轴上方,且 是等腰直角三角形,求
是等腰直角三角形,求 点坐标;
点坐标;
(2)若直线 的斜率乘积为
的斜率乘积为 ,求
,求 点坐标
点坐标 满足的关系式。
满足的关系式。
(1) (2)
(2)
解析试题分析:(1)因为 是等腰直角三角形,没说哪个角为直角,所以需分三种情况讨论。当
是等腰直角三角形,没说哪个角为直角,所以需分三种情况讨论。当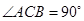 时,点C在线段AB的中垂线上,即点C横坐标为0,所以可设点C
时,点C在线段AB的中垂线上,即点C横坐标为0,所以可设点C ,因为
,因为 在x轴上方,所以
在x轴上方,所以 。,根据两直线垂直斜率相乘等于
。,根据两直线垂直斜率相乘等于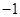 ,求出
,求出 。当
。当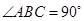 时,
时, ,且两直角边相等,即
,且两直角边相等,即 ,所以
,所以 。当
。当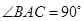 时,即
时,即 ,且
,且 ,所以
,所以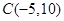 。(2)根据斜率公式列出方程,详见解析。
。(2)根据斜率公式列出方程,详见解析。
试题解析:(1)因为 是等腰直角三角形,当
是等腰直角三角形,当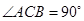 时,设点C
时,设点C 且
且 ,所以直线AC的斜率
,所以直线AC的斜率 ,直线BC的斜率
,直线BC的斜率 ,因为
,因为 ,所以
,所以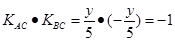 ,所以
,所以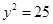 ,因为
,因为 ,所以
,所以 ,此时点
,此时点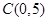 。
。
当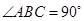 时,
时, ,且两直角边相等,即
,且两直角边相等,即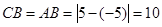 ,所以
,所以 。
。
当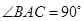 时,即
时,即 ,且
,且 ,所以
,所以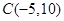 。综上可得点
。综上可得点 坐标为
坐标为 或
或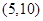 或
或 
(2)直线AC斜率为
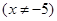 ,直线BC斜率为
,直线BC斜率为
 ,由题意可得
,由题意可得
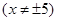 ,整理的
,整理的
考点:分类讨论思想,求轨迹问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x上时,求直线AB的方程.
x上时,求直线AB的方程.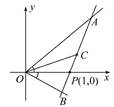
 :
: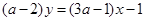
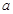 取何值,直线
取何值,直线 ,且直线L在x轴上的截距等于在y轴上的截距的2倍,求直线L的方程.
,且直线L在x轴上的截距等于在y轴上的截距的2倍,求直线L的方程. 经过直线
经过直线 与直线
与直线 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
.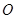 对称的直线方程.
对称的直线方程. 的交点M,且满足下列条件的直线方程:
的交点M,且满足下列条件的直线方程: 的顶点
的顶点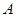 的坐标为
的坐标为 ,
, 边上的中线所在直线方程为
边上的中线所在直线方程为 的平分线所在直线方程为
的平分线所在直线方程为 ,求
,求 边所在直线的方程。
边所在直线的方程。