题目内容
已知直线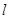 :
: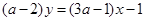
(Ⅰ)求证:不论实数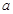 取何值,直线
取何值,直线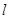 总经过一定点.
总经过一定点.
(Ⅱ)若直线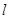 与两坐标轴的正半轴围成的三角形面积最大,求
与两坐标轴的正半轴围成的三角形面积最大,求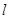 的方程.
的方程.
(Ⅰ)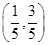 ;(Ⅱ)
;(Ⅱ)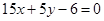 .
.
解析试题分析:(Ⅰ)直线方程整理得: ,可知该直线过直线
,可知该直线过直线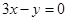 与直线
与直线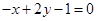 的交点.经过解方程组
的交点.经过解方程组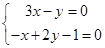 ,可得到定点为
,可得到定点为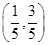 ;(Ⅱ)由题知
;(Ⅱ)由题知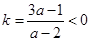 则
则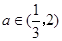 令
令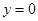 则
则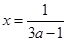 ,令
,令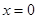 则
则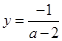 .求出与坐标轴的截距后再根据三角形的面积公式得到
.求出与坐标轴的截距后再根据三角形的面积公式得到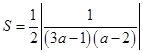 ,要使得
,要使得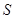 最大,就是当
最大,就是当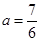 时三角形的面积最大.此时可以得到
时三角形的面积最大.此时可以得到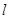 的方程为:
的方程为: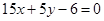 .
.
试题解析:(Ⅰ)由直线方程整理得: ,所以可知该直线过直线
,所以可知该直线过直线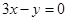 与直线
与直线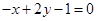 的交点.解方程组
的交点.解方程组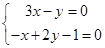 可得
可得 .所以直线
.所以直线 过定点
过定点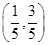 .
.
(Ⅱ)由题知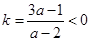 ,则
,则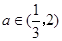 .令
.令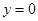 ,则
,则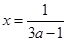 ,即为直线在
,即为直线在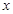 轴上的截距;
轴上的截距;
令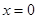 ,则
,则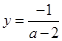 .即为直线在
.即为直线在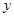 轴上的截距.
轴上的截距.
所以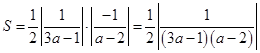 .
.
要使得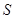 最大,就是当
最大,就是当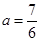 时三角形的面积最大.所以直线
时三角形的面积最大.所以直线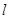 的方程为:
的方程为: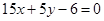 .
.
考点:(Ⅰ)直线系方程;(Ⅱ)直线的截距式方程.

练习册系列答案
相关题目
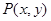 满足到定点
满足到定点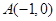 的距离与到定点
的距离与到定点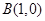 距离之比为
距离之比为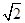 .
.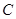 的方程;
的方程;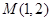 的直线
的直线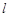 与曲线
与曲线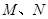 ,若
,若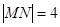 ,求直线
,求直线 的最大值与最小值.
的最大值与最小值.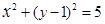 ,直线
,直线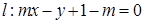 .
.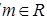 ,直线
,直线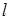 与圆C总有两个不同的交点;
与圆C总有两个不同的交点; ,求
,求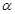 过坐标原点
过坐标原点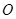 ,
,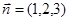 是平面
是平面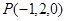 到平面
到平面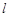 过
过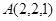 ,
,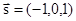 是直线
是直线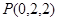 到直线
到直线 的距离.
的距离. ,且和圆C:
,且和圆C: 相交,截得弦长为
相交,截得弦长为 ,求l的方程.
,求l的方程. ,
, 为动点
为动点 是等腰直角三角形,求
是等腰直角三角形,求 的斜率乘积为
的斜率乘积为 ,求
,求 满足的关系式。
满足的关系式。 的顶点A(0,1),AB边上的中线CD所在直线方程为
的顶点A(0,1),AB边上的中线CD所在直线方程为 ,AC边上的高BH所在直线方程为
,AC边上的高BH所在直线方程为 .
. 与
与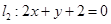 的交点
的交点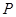 ,求:(1)过点
,求:(1)过点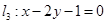 的直线
的直线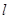 的方程。
的方程。