题目内容
已知直线 :
: ,直线
,直线 :
: ,其中
,其中 ,
, .
.
(1)求直线 的概率;
的概率;
(2)求直线 与
与 的交点位于第一象限的概率.
的交点位于第一象限的概率.
 :
: ,直线
,直线 :
: ,其中
,其中 ,
, .
.(1)求直线
 的概率;
的概率;(2)求直线
 与
与 的交点位于第一象限的概率.
的交点位于第一象限的概率.(1) (2)
(2)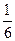
 (2)
(2)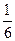
(1)解:直线 的斜率
的斜率 ,直线
,直线 的斜率
的斜率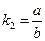 .
.
设事件 为“直线
为“直线 ”.
”.
 ,
, 的总事件数为
的总事件数为 ,
, ,…,
,…, ,
, ,
, ,…,
,…, ,…,
,…,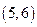 ,
, 共36种.
共36种.
若 ,则
,则 ,即
,即 ,即
,即 .
.
满足条件的实数对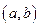 有
有 、
、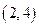 、
、 共三种情形.
共三种情形.
所以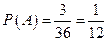 .
.
答:直线 的概率为
的概率为 .
.
(2)解:设事件 为“直线
为“直线 与
与 的交点位于第一象限”,由于直线
的交点位于第一象限”,由于直线 与
与 有交点,则
有交点,则 .
.
联立方程组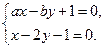 解得
解得
因为直线 与
与 的交点位于第一象限,则
的交点位于第一象限,则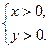
即 解得
解得 .
.
 ,
, 的总事件数为
的总事件数为 ,
, ,…,
,…, ,
, ,
, ,…,
,…, ,…,
,…,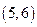 ,
, 共36种.
共36种.
满足条件的实数对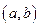 有
有 、
、 、
、 、
、 、
、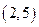 、
、 共六种.
共六种.
所以 .
.
答:直线 与
与 的交点位于第一象限的概率为
的交点位于第一象限的概率为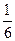 .
.
 的斜率
的斜率 ,直线
,直线 的斜率
的斜率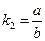 .
.设事件
 为“直线
为“直线 ”.
”. ,
, 的总事件数为
的总事件数为 ,
, ,…,
,…, ,
, ,
, ,…,
,…, ,…,
,…,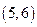 ,
, 共36种.
共36种.若
 ,则
,则 ,即
,即 ,即
,即 .
.满足条件的实数对
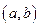 有
有 、
、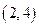 、
、 共三种情形.
共三种情形.所以
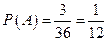 .
.答:直线
 的概率为
的概率为 .
.(2)解:设事件
 为“直线
为“直线 与
与 的交点位于第一象限”,由于直线
的交点位于第一象限”,由于直线 与
与 有交点,则
有交点,则 .
.联立方程组
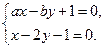 解得
解得
因为直线
 与
与 的交点位于第一象限,则
的交点位于第一象限,则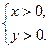
即
 解得
解得 .
. ,
, 的总事件数为
的总事件数为 ,
, ,…,
,…, ,
, ,
, ,…,
,…, ,…,
,…,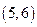 ,
, 共36种.
共36种.满足条件的实数对
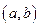 有
有 、
、 、
、 、
、 、
、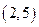 、
、 共六种.
共六种.所以
 .
.答:直线
 与
与 的交点位于第一象限的概率为
的交点位于第一象限的概率为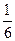 .
.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 系列的情况如下表:
系列的情况如下表:

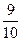

 的分布列及其数学期望
的分布列及其数学期望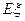 .
.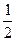 ,且面试是否合格互不影响。求:
,且面试是否合格互不影响。求: 和
和 。
。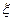 表示购得不合格食品的件数,试写出
表示购得不合格食品的件数,试写出 ,回答第三题正确的概率为
,回答第三题正确的概率为 ,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为
,且各题回答正确与否相互之间没有影响.记这位挑战者回答这三个问题的总得分为 。
。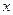 和该年支出维修费用
和该年支出维修费用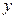 (万元),得到数据如下:
(万元),得到数据如下: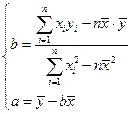 )
)