题目内容
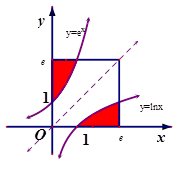
设函数f(x)=ex+sinx,g(x)=x-2;
(1)求证:函数y=f(x)在[0,+∞)上单调递增;
(2)设P(x1,f(x1)),Q(x2,g(x2))(x1≥0,x2>0),若直线PQ∥x轴,求P,Q两点间的最短距离.
(1)求证:函数y=f(x)在[0,+∞)上单调递增;
(2)设P(x1,f(x1)),Q(x2,g(x2))(x1≥0,x2>0),若直线PQ∥x轴,求P,Q两点间的最短距离.
(1)证明:x≥0时,f'(x)=ex+cosx≥1+cosx≥0,
所以函数y=f(x)在[0,+∞)上单调递增;---------------------------(6分)
(2)因为f(x1)=g(x2),所以ex1+sinx1=x2-2---------------------(8分)
所以P,Q两点间的距离等于|x2-x1|=|ex1+sinx1-x1+2|,------(9分)
设h(x)=ex+sinx-x+2(x≥0),则h'(x)=ex+cosx-1(x≥0),
记l(x)=h'(x)=ex+cosx-1(x≥0),则l'(x)=ex-sinx≥1-sinx≥0,
所以h'(x)≥h'(0)=1>0,------------------------------------(12分)
所以h(x)在[0,+∞)上单调递增,所以h(x)≥h(0)=3------------(14分)
所以|x2-x1|≥3,即P,Q两点间的最短距离等于3.---------------(15分)
所以函数y=f(x)在[0,+∞)上单调递增;---------------------------(6分)
(2)因为f(x1)=g(x2),所以ex1+sinx1=x2-2---------------------(8分)
所以P,Q两点间的距离等于|x2-x1|=|ex1+sinx1-x1+2|,------(9分)
设h(x)=ex+sinx-x+2(x≥0),则h'(x)=ex+cosx-1(x≥0),
记l(x)=h'(x)=ex+cosx-1(x≥0),则l'(x)=ex-sinx≥1-sinx≥0,
所以h'(x)≥h'(0)=1>0,------------------------------------(12分)
所以h(x)在[0,+∞)上单调递增,所以h(x)≥h(0)=3------------(14分)
所以|x2-x1|≥3,即P,Q两点间的最短距离等于3.---------------(15分)

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 (
(