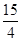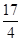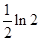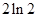题目内容
函数f(x)=
+lnx,其中a为实常数.
(1)讨论f(x)的单调性;
(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围;
(3)若a=0,设g(n)=1+
+
+…+
,h(n)=
+
+
+…+
(n≥2,n∈N+).是否存在实常数b,既使g(n)-f(n)>b又使h(n)-f(n+1)<b对一切n≥2,n∈N+恒成立?若存在,试找出b的一个值,并证明;若不存在,说明理由.
| a |
| x |
(1)讨论f(x)的单调性;
(2)不等式f(x)≥1在x∈(0,1]上恒成立,求实数a的取值范围;
(3)若a=0,设g(n)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 23 |
| 2 |
| 32 |
| 3 |
| 43 |
| n-1 |
| n3 |
(1)定义域为(0,+∞),
①当a≤0时,函数在定义域上单调增函数;
②当a>0时,f′(x)=-
+
,当x>a时,f′(x)>0,函数单调递增,增区间为(a,+∞);当0<x<a时,f′(x)<0,函数单调递减,单调减区间为(0,a);
(2)不等式f(x)≥1在x∈(0,1]上恒成立,?a≥[-xlnx+x]max,x∈(0,1],
令g(x)=-xlnx+x,x∈(0,1],g′(x)=-lnx-x•
+1=-lnx≥0(x∈(0,1]),
∴g(x)在x∈(0,1]上单增,
∴g(x)max=g(1)=1,
∴a≥1,
故a的取值范围为[1,+∞).
(3)存在,如b=0等.下面证明:1+
+
+…+
>lnn,(n≥2,n∈N+)
及
+
+
+…+
<ln(n+1),(n≥2,n∈N+)成立.
①先证1+
+
+…+
>lnn,(n∈N+),注意lnn=ln
+ln
+…+ln
,
这只要证
>ln
=ln(1+
),(k=2,3,…n)(*)即可,
x>ln(1+x)对x>0恒成立,取x=
(k≥2)即可得上式成立.
让k=2,3,…,n分别代入(*)式再相加即证:1+
+
+…+
>lnn,(n∈N+),
于是1+
+
+…+
+
>1+
+
+…+
>lnn,(n∈N+).
②再证
+
+
+…+
<ln(n+1),(n≥2,n∈N+),
∵
<
=
=
<
=
-
,(n≥2),
∴
+
+
+…+
<(
-
)+(
-
)+…+(
-
)=
-
<
,
又∵n≥2,ln(n+1)≥ln3>ln
=
,故不等式成立.
①当a≤0时,函数在定义域上单调增函数;
②当a>0时,f′(x)=-
| a |
| x2 |
| 1 |
| x |
(2)不等式f(x)≥1在x∈(0,1]上恒成立,?a≥[-xlnx+x]max,x∈(0,1],
令g(x)=-xlnx+x,x∈(0,1],g′(x)=-lnx-x•
| 1 |
| x |
∴g(x)在x∈(0,1]上单增,
∴g(x)max=g(1)=1,
∴a≥1,
故a的取值范围为[1,+∞).
(3)存在,如b=0等.下面证明:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
及
| 1 |
| 23 |
| 2 |
| 33 |
| 3 |
| 43 |
| n-1 |
| n3 |
①先证1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 2 |
| 1 |
| 3 |
| 2 |
| n |
| n-1 |
这只要证
| 1 |
| k-1 |
| k |
| k-1 |
| 1 |
| k-1 |
x>ln(1+x)对x>0恒成立,取x=
| 1 |
| k-1 |
让k=2,3,…,n分别代入(*)式再相加即证:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
于是1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
②再证
| 1 |
| 23 |
| 2 |
| 33 |
| 3 |
| 43 |
| n-1 |
| n3 |
∵
| n-1 |
| n3 |
| n-1 |
| n3-1 |
| n-1 |
| (n-1)(n2+n+1) |
| 1 |
| n2+n+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| 23 |
| 2 |
| 33 |
| 3 |
| 43 |
| n-1 |
| n3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
又∵n≥2,ln(n+1)≥ln3>ln
| e |
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

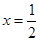 ,
,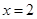 ,曲线
,曲线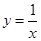 及
及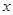 轴所围成的图形的面积是( )
轴所围成的图形的面积是( )