题目内容
已知函数f(x)=x2–(m+1)x+m(m∈R)
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角 求证:m≥5;
求证:m≥5;
(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角
 求证:m≥5;
求证:m≥5;(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
(1)证明:f(x)+4=0即x2–(m+1)x+m+4="0. " 依题意:
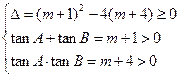
又A、B锐角为三角形内两内角
∴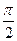 <A+B<π
<A+B<π
∴tan(A+B)<0,即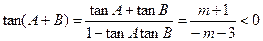
∴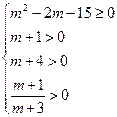 ∴m≥5
∴m≥5
(2)证明: ∵f(x)=(x–1)(x–m)
又–1≤cosα≤1,∴1≤2+cosα≤3,恒有f(2+cosα)≤0
即1≤x≤3时,恒有f(x)≤0即(x–1)(x–m)≤0
∴m≥x但xmax=3,∴m≥xmax=3
(3)解:
∵f(sinα)=sin2α–(m+1)sinα+m=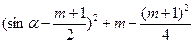
且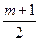 ≥2,
≥2,
∴当sinα=–1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3
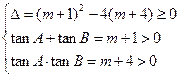
又A、B锐角为三角形内两内角
∴
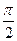 <A+B<π
<A+B<π∴tan(A+B)<0,即
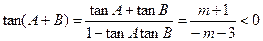
∴
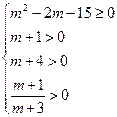 ∴m≥5
∴m≥5(2)证明: ∵f(x)=(x–1)(x–m)
又–1≤cosα≤1,∴1≤2+cosα≤3,恒有f(2+cosα)≤0
即1≤x≤3时,恒有f(x)≤0即(x–1)(x–m)≤0
∴m≥x但xmax=3,∴m≥xmax=3
(3)解:
∵f(sinα)=sin2α–(m+1)sinα+m=
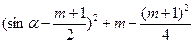
且
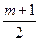 ≥2,
≥2,∴当sinα=–1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
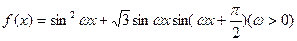
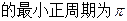 (1)求
(1)求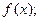
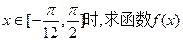 的值域。
的值域。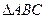 中,角
中,角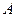 、
、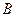 、
、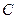 的对边分别为
的对边分别为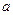 、
、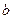 、
、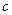 ,且
,且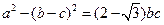 ,
,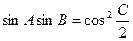 ,
,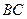 边上中线
边上中线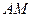 的长为
的长为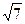 .
.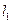 、
、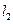 、
、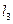 是同一平面内三条不重合自上而下的平行直线.
是同一平面内三条不重合自上而下的平行直线.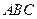 的三顶点分别放在
的三顶点分别放在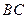 和
和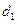 ,
,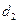 ,求
,求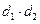 的范围?
的范围?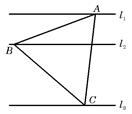
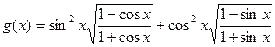 ,其中
,其中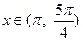 ,求函数
,求函数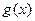 的值域.
的值域. 中,
中, ,
,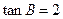 ,求
,求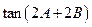 的值.
的值.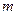 的值;
的值; 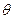 的值
的值