题目内容
表1中数阵称为“森德拉姆筛”,其特点是每行每列都是等差数列,则表中数字206共出现 次。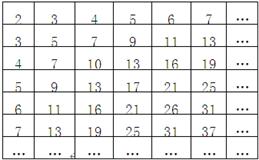

4
试题分析:第1行数组成的数列A1j(j=1,2,…)是以2为首项,公差为1的等差数列,第j列数组成的数列A1j(i=1,2,)是以j+1为首项,公差为j的等差数列,求出通项公式,可以求出结果.第i行第j列的数记为Aij.那么每一组i与j的解就是表中一个数.
因为第一行数组成的数列A1j(j=1,2,…)是以2为首项,公差为1的等差数列,
所以A1j=2+(j-1)×1=j+1,
所以第j列数组成的数列A1j(i=1,2,…)是以j+1为首项,公差为j的等差数列,
所以Aij=(j+1)+(i-1)×j=ij+1.
令Aij=ij+1=206,
即ij=205=1×205=5×41=41×5=205×1,
所以,表中206共出现4次.
故答案为:4.
点评:解决该试题的关键是灵活运用公式得到Aij=(j+1)+(i-1)×j=ij+1求解运算得到结论。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
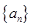 中,
中,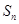 是数列
是数列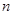 项和,
项和,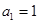 ,当
,当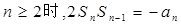
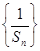 是等差数列;
是等差数列;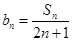 求数列
求数列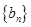 的前
的前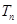 ;
;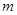 ,使得对任意自然数
,使得对任意自然数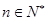 ,都有
,都有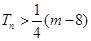 成立?若存在,求出
成立?若存在,求出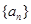 的前
的前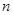 项和
项和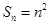 。(1)求数列
。(1)求数列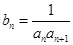 ,且数列
,且数列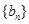 的前
的前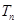 。若
。若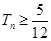 ,求
,求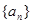 中,
中,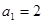 ,
,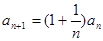 ,则
,则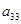 =________________
=________________
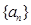 的前
的前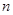 项和
项和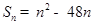 。
。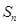 的最大或最小值。
的最大或最小值。 }中
}中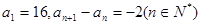 ,则数列
,则数列 的前n项和
的前n项和 最大时,n的值为 ( )
最大时,n的值为 ( ) 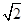
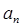 }的前n项和
}的前n项和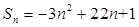 ,
,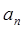 |}的前n项和
|}的前n项和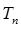 .
.