题目内容
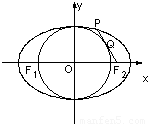 如图,已知F1,F2是椭圆
如图,已知F1,F2是椭圆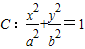 (a>b>0)的左、右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q为线段PF2的中点,则椭圆C的离心率为( )
(a>b>0)的左、右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q为线段PF2的中点,则椭圆C的离心率为( )A.
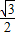
B.
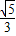
C.
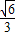
D.
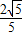
【答案】分析:连接OQ,PF1,先利用三角形中位线定理证明OQ∥PF1,OQ= PF1,而OQ即为圆的半径b,从而得焦半径PF1=2b,再利用椭圆的定义,得PF2=2a-2b,最后利用直线与圆相切的几何性质,证明PF1⊥PF2,从而在三角形中利用勾股定理得到a、b、c间的等式,进而计算离心率即可
PF1,而OQ即为圆的半径b,从而得焦半径PF1=2b,再利用椭圆的定义,得PF2=2a-2b,最后利用直线与圆相切的几何性质,证明PF1⊥PF2,从而在三角形中利用勾股定理得到a、b、c间的等式,进而计算离心率即可
解答: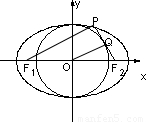 解:如图:连接OQ,PF1,∵点Q为线段PF2的中点,∴OQ∥PF1,OQ=
解:如图:连接OQ,PF1,∵点Q为线段PF2的中点,∴OQ∥PF1,OQ= PF1,
PF1,
∴PF1=2OQ=2b,
由椭圆定义,PF1+PF2=2a,∴PF2=2a-2b
∵线段PF2与圆x2+y2=b2相切于点Q,
∴OQ⊥PF2,
∴PF1⊥PF2,且|F1F2|=2c,
∴(2b)2+(2a-2b)2=(2c)2
即3b=2a,5a2=9c2,
∴e=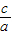 =
=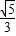
故选 B
点评:本题主要考查了椭圆的定义及其运用,直线与圆的位置关系,椭圆的几何性质及其离心率的求法,属基础题
 PF1,而OQ即为圆的半径b,从而得焦半径PF1=2b,再利用椭圆的定义,得PF2=2a-2b,最后利用直线与圆相切的几何性质,证明PF1⊥PF2,从而在三角形中利用勾股定理得到a、b、c间的等式,进而计算离心率即可
PF1,而OQ即为圆的半径b,从而得焦半径PF1=2b,再利用椭圆的定义,得PF2=2a-2b,最后利用直线与圆相切的几何性质,证明PF1⊥PF2,从而在三角形中利用勾股定理得到a、b、c间的等式,进而计算离心率即可解答:
 解:如图:连接OQ,PF1,∵点Q为线段PF2的中点,∴OQ∥PF1,OQ=
解:如图:连接OQ,PF1,∵点Q为线段PF2的中点,∴OQ∥PF1,OQ= PF1,
PF1,∴PF1=2OQ=2b,
由椭圆定义,PF1+PF2=2a,∴PF2=2a-2b
∵线段PF2与圆x2+y2=b2相切于点Q,
∴OQ⊥PF2,
∴PF1⊥PF2,且|F1F2|=2c,
∴(2b)2+(2a-2b)2=(2c)2
即3b=2a,5a2=9c2,
∴e=
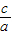 =
=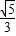
故选 B
点评:本题主要考查了椭圆的定义及其运用,直线与圆的位置关系,椭圆的几何性质及其离心率的求法,属基础题

练习册系列答案
相关题目
 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆 如图,已知F1,F2是椭圆C:
如图,已知F1,F2是椭圆C: (2012•鹰潭一模)如图,已知F1,F2是椭圆
(2012•鹰潭一模)如图,已知F1,F2是椭圆 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆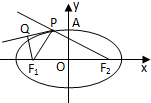 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆