题目内容
 如图,已知F1,F2是椭圆C:
如图,已知F1,F2是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
分析:本题考察的知识点是平面向量的数量积的运算,及椭圆的简单性质,由F1、F2是椭圆 C:
+
=1(a>b>0)的左、右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,且点Q为线段PF2的中点,连接OQ,F1P后,我们易根据平面几何的知识,根据切线的性质及中位线的性质得到PF2⊥PF1,并由此得到椭圆C的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
解答: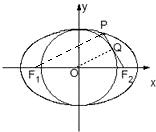 解:连接OQ,F1P如下图所示:
解:连接OQ,F1P如下图所示:
则由切线的性质,则OQ⊥PF2,
又由点Q为线段PF2的中点,O为F1F2的中点
∴OQ∥F1P
∴PF2⊥PF1,
故|PF2|=2a-2b,
且|PF1|=2b,|F1F2|=2c,
则|F1F2|2=|PF1|2+|PF2|2
得4c2=4b2+4(a2-2ab+b2)
解得:b=
a
则c=
a
故椭圆的离心率为:
故答案为:
.
 解:连接OQ,F1P如下图所示:
解:连接OQ,F1P如下图所示:则由切线的性质,则OQ⊥PF2,
又由点Q为线段PF2的中点,O为F1F2的中点
∴OQ∥F1P
∴PF2⊥PF1,
故|PF2|=2a-2b,
且|PF1|=2b,|F1F2|=2c,
则|F1F2|2=|PF1|2+|PF2|2
得4c2=4b2+4(a2-2ab+b2)
解得:b=
| 2 |
| 3 |
则c=
| ||
| 3 |
故椭圆的离心率为:
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题涉及等量关系转为不等关系,在与所求量有关的参量上作文章是实现转化的关键,还有离心率的求解问题,关键是根据题设条件获得关于a,b,c的关系式,最后化归为a,c(或e)的关系式,利用方程求解.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆 (2012•鹰潭一模)如图,已知F1,F2是椭圆
(2012•鹰潭一模)如图,已知F1,F2是椭圆 如图,已知F1、F2分别为椭圆
如图,已知F1、F2分别为椭圆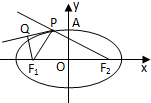 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆