Question

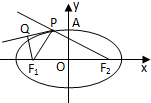如图，已知F₁、F₂是椭圆

x2

172

+

y2

152

=1的左、右焦点，A是椭圆短轴的一个端点，P是椭圆上任意一点，过F₁引∠F₁PF₂的外角平分线的垂线，垂足为Q，则|AQ|的最大值为

 

．

Answer 1

分析：点F₁关于∠F₁PF₂的外角平分线PQ的对称点M在直线F₂Q的延长线上，故|F₂M|=|PF₁|+|PF₂|=2a=34，又OQ是△F₂F₁M的中位线，故|OQ|=17，由此可以判断出点Q的轨迹，进而可求|AQ|的最大值．

解答：解：点F₁关于∠F₁PF₂的外角平分线PQ的对称点M在直线F₂Q的延长线上，
故|F₂M|=|PF₁|+|PF₂|=2a=34，
又OQ是△F₂F₁M的中位线，故|OQ|=17，
∴点Q的轨迹是以原点为圆心，17为半径的圆，
∵A是椭圆短轴的一个端点，b=15，
∴|AQ|的最大值为17+15=32．
故答案为：32．

点评：本题给出椭圆上动点P，求点M的轨迹方程，着重考查了椭圆的定义和简单几何性质，以及等腰三角形“三线合一”等知识，属于中档题．