题目内容
在计算机的算法语言中有一种函数[x]叫做高斯函数,它表示数x的整数部分(即小于等于x的最大整数,如[3.15]=3,[0.7]=0,[-2.6]=-3)设函数f(x)=
(a>0,且a≠1),则函数y=[f(x)-
]+[f(-x)-
]的值域为( )
| ax |
| 1+ax |
| 1 |
| 2 |
| 1 |
| 2 |
| A、{-1,0} |
| B、{0} |
| C、{-1} |
| D、{-1,0,1} |
分析:本填空题利用特殊值法解决,取a=2,由题意知,f(x)-
=
-
是定义域R上的奇函数,且值域是(-
,
);
∴f(-x)的值域也是(-
,
);分x=0,x>0,x<0时讨论函数y的值即可.
| 1 |
| 2 |
| 2x |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(-x)的值域也是(-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意,g(x)=f(x)-
=
-
=1-
-
=
-
;f(-x)=
-
=
-
;
∴g(-x)=-g(x),即g(x)是奇函数.
又∵2x>0,∴1+2x>1,∴0 <
< 1,∴-
<
-
<
;
即 -
<g(-x)<
.所以,-
<g(x)<
.
当x=0时,g(x)=g(-x)=0,y=[g(x)]+[g(-x)]=0;
当x≠0时,若x>0,则0<g(x)<
,-
<g(-x)<0,
∴y=[g(x)]+[g(-x)]=0+(-1)=-1,
若x<0,则y=[g(x)]+[g(-x)]=(-1)+0=-1.
所以函数y的值域为{0,-1}.
故选A.
| 1 |
| 2 |
| 2x |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 2-x |
| 1+2-x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
∴g(-x)=-g(x),即g(x)是奇函数.
又∵2x>0,∴1+2x>1,∴0 <
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
即 -
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x=0时,g(x)=g(-x)=0,y=[g(x)]+[g(-x)]=0;
当x≠0时,若x>0,则0<g(x)<
| 1 |
| 2 |
| 1 |
| 2 |
∴y=[g(x)]+[g(-x)]=0+(-1)=-1,
若x<0,则y=[g(x)]+[g(-x)]=(-1)+0=-1.
所以函数y的值域为{0,-1}.
故选A.
点评:本题用求值域来考查指数函数的性质,函数的奇偶性,函数取整问题,应该是有难度的小题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
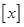 叫做取整函数(也叫高斯函数).它表示x的整数部分,即表示不超过x的最大整数.如
叫做取整函数(也叫高斯函数).它表示x的整数部分,即表示不超过x的最大整数.如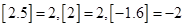 .设函数
.设函数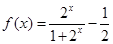 ,则函数
,则函数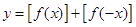 的值域为 .
的值域为 .