题目内容
在计算机的算法语言中有一种函数[x]叫做取整函数(也称高斯函数),表示不超过x的最大整数,例如[2]=2,[3.3]=3,[-2.4]=-3,设函数f(x)=
-
,则函数y=[f(x)]+[f(-x)]的值域为
| 2x |
| 1+2x |
| 1 |
| 2 |
{0,-1}
{0,-1}
.分析:由题意得,函数f(x)=
-
是定义在R上的奇函数,值域为(-
,
),且f(-x)的值域也是(-
,
);分x>0,x=0,x<0时讨论函数y的值即可.
| 2x |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由题意,∵函数f(x)=
-
,∴f(-x)=
-
=
-
;
∴f(-x)=-f(x),∴f(x)为奇函数.
又∵2x>0,∴1+2x>1,∴0<
<1,∴-
<
-
<
.
即-
<f(-x)<
,∴-
<f(x)<
.
当x=0时,f(x)=f(-x)=0,y=[f(x)]+[f(-x)]=0;
当x≠0时,若x>0,0<f(x)<
,-
<f(-x)<0
∴y=[f(x)]+[f(-x)]=0+(-1)=-1;
若x<0,y=[f(x)]+[f(-x)]=(-1)+0=-1,
∴函数y的值域为{0,-1}.
故答案应为{0,-1}.
| 2x |
| 1+2x |
| 1 |
| 2 |
| 2-x |
| 1+2-x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
∴f(-x)=-f(x),∴f(x)为奇函数.
又∵2x>0,∴1+2x>1,∴0<
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
即-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x=0时,f(x)=f(-x)=0,y=[f(x)]+[f(-x)]=0;
当x≠0时,若x>0,0<f(x)<
| 1 |
| 2 |
| 1 |
| 2 |
∴y=[f(x)]+[f(-x)]=0+(-1)=-1;
若x<0,y=[f(x)]+[f(-x)]=(-1)+0=-1,
∴函数y的值域为{0,-1}.
故答案应为{0,-1}.
点评:本题以高斯函数为素材,用求值域来考查指数函数的性质、函数的奇偶性、函数的取整问题,有一定的技巧性.

练习册系列答案
相关题目
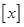 叫做取整函数(也叫高斯函数).它表示x的整数部分,即表示不超过x的最大整数.如
叫做取整函数(也叫高斯函数).它表示x的整数部分,即表示不超过x的最大整数.如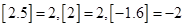 .设函数
.设函数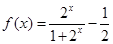 ,则函数
,则函数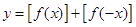 的值域为 .
的值域为 .