题目内容
若曲线f（x）=ax2+lnx存在垂直于y轴的切线，则实数a取值范围是
- A.a≠0
- B.a≥0
- C.a＜0
- D.a∈R
C
分析：由曲线f（x）=ax2+lnx存在垂直于y轴的切线，故f′（x）=0有实数解，解出a的取值范围即可．
解答：∵曲线f（x）=ax2+lnx存在垂直于y轴的切线，（x＞0）
∴
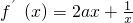=0有解，得
，
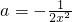∵x＞0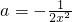，∴＜0，
∴实数a的取值范围是a＜0．
故选C．
点评：理解导数的几何意义是解题的关键．
分析：由曲线f（x）=ax2+lnx存在垂直于y轴的切线，故f′（x）=0有实数解，解出a的取值范围即可．
解答：∵曲线f（x）=ax2+lnx存在垂直于y轴的切线，（x＞0）
∴
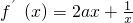=0有解，得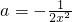，∵x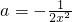＞0，∴
＜0，∴实数a的取值范围是a＜0．
故选C．
点评：理解导数的几何意义是解题的关键．
练习册系列答案
相关题目
若曲线f（x）=x•sinx+1在x=
处的切线与直线ax+2y+1=0互相垂直，则实数a等于（ ）
| π |
| 2 |
| A、-2 | B、-1 | C、1 | D、2 |