题目内容
20.已知数列{an}满足a1=1,an+1=(n2+n-λ)an(n=1,2,…),λ是常数.(1)当a2=-1时,求λ及a3的值;
(2)是否存在实数λ使数列{an}为等差数列?若存在,求出λ及数列{an}的通项公式,若不存在,请说明理由.
分析 (1)利用a2的值列出关于λ的方程,进而求出λ的值,再根据a2的值计算出a3的值;
(2)通过假设数列{an}可能为等差数列,利用该数列的前3项成等差数列得出关于λ的方程,进而确定出λ的值,验证数列后面的项是否满足等差数列即可.
解答 解:(1)∵an+1=(n2+n-λ)an(n=1,2,…),且a1=1,
∴当a2=-1时,得-1=2-λ,即λ=3,
∴a3=(22+2-3)×(-1)=-3.
(2)结论:不存在实数λ使数列{an}为等差数列.
理由如下:
∵a1=1,an+1=(n2+n-λ)an,
∴a2=2-λ,a3=(6-λ)(2-λ),a4=(12-λ)(6-λ)(2-λ).
假设存在λ使{an}为等差数列,则a3-a2=a2-a1,
即(5-λ)(2-λ)=1-λ,解得λ=3.
于是a2-a1=1-λ=-2,
a4-a3=(11-λ)(6-λ)(2-λ)=-24.
这与{an}为等差数列矛盾.
综上,对任意λ数列{an}都不可能是等差数列.
点评 本题考查数列递推关系确定数列的问题,考查数列为等差数列的判定方法、探究性问题的解决思路,考查学生解决问题的方程思想、确定一个命题为假命题的方法,关键要进行问题的转化,考查学生的运算能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
11.执行如图所示的程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )
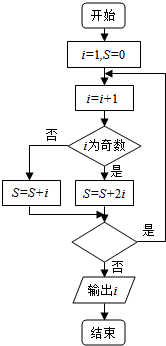

| A. | S≤10? | B. | S≤12? | C. | S≤14? | D. | S≤16? |
8.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
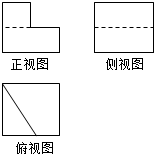

| A. | 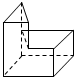 | B. | 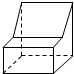 | C. |  | D. |  |