题目内容
(本小题满分12分)
设函数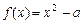 .
.
(1)当 时,求函数
时,求函数 在区间
在区间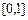 上的最小值;
上的最小值;
(2)当 时,曲线
时,曲线 在点
在点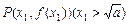 处的切线为
处的切线为 ,
, 与
与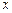 轴交于点
轴交于点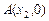
求证: .
.
设函数
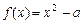 .
.(1)当
 时,求函数
时,求函数 在区间
在区间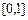 上的最小值;
上的最小值;(2)当
 时,曲线
时,曲线 在点
在点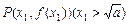 处的切线为
处的切线为 ,
, 与
与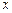 轴交于点
轴交于点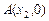
求证:
 .
.(1)当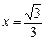 时,
时,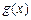 有最小值
有最小值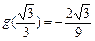
(2)略
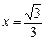 时,
时,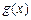 有最小值
有最小值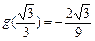
(2)略
解:(1) 时,
时,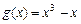 ,由
,由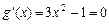 ,解得
,解得 ……………(2分)
……………(2分)
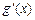 的变化情况如下表:
的变化情况如下表:
…………(4分)
所以当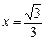 时,
时,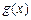 有最小值
有最小值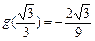 …………………………………(5分)
…………………………………(5分)
(2)证明:曲线 在点
在点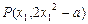 处的切线斜率
处的切线斜率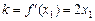
曲线 在点P处的切线方程为
在点P处的切线方程为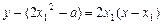 ………………(7分)
………………(7分)
令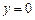 ,得
,得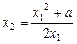 ,∴
,∴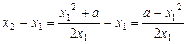
∵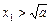 ,∴
,∴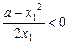 ,即
,即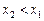 ……………………………………………(9分)
……………………………………………(9分)
又∵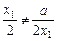 ,∴
,∴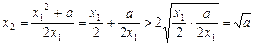
所以 ………………………………………………………(12分)
………………………………………………………(12分)
 时,
时,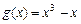 ,由
,由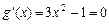 ,解得
,解得 ……………(2分)
……………(2分)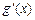 的变化情况如下表:
的变化情况如下表: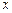 | 0 | 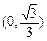 | 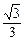 | 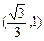 | 1 |
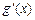 | | - | 0 | + | |
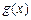 | 0 | ↘ | 极小值 | ↗ | 0 |
所以当
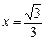 时,
时,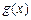 有最小值
有最小值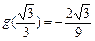 …………………………………(5分)
…………………………………(5分)(2)证明:曲线
 在点
在点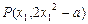 处的切线斜率
处的切线斜率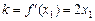
曲线
 在点P处的切线方程为
在点P处的切线方程为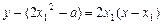 ………………(7分)
………………(7分)令
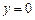 ,得
,得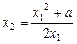 ,∴
,∴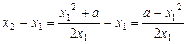
∵
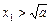 ,∴
,∴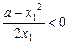 ,即
,即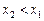 ……………………………………………(9分)
……………………………………………(9分)又∵
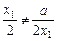 ,∴
,∴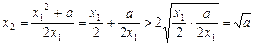
所以
 ………………………………………………………(12分)
………………………………………………………(12分)
练习册系列答案
相关题目
 的图象过点(0,-3),且
的图象过点(0,-3),且 的解集
的解集 .
.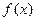 的解析式;
的解析式; 的最值.
的最值.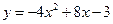 。
。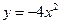 的图像经过怎样平移得来;
的图像经过怎样平移得来; )求函数的最大值或最小值;
)求函数的最大值或最小值;
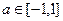 ,函数
,函数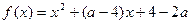 的值恒大于零,求
的值恒大于零,求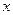 的取值范围。
的取值范围。 上是增函数.
上是增函数.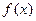 满足:
满足: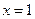 时有极值;
时有极值;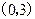 ,且在该点处的切线与直线
,且在该点处的切线与直线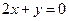 平行.求
平行.求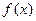 是一次函数,且
是一次函数,且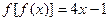 ,则
,则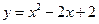 与
与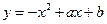
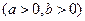 在它们的一个交点处切线互相垂直,则
在它们的一个交点处切线互相垂直,则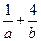 的最小值为( )
的最小值为( ) 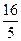
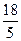
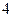
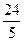
 设函数
设函数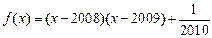 ,有 ( )
,有 ( )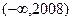 、
、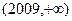 内;
内;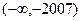 、
、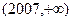 内; 高#考#资#源#
内; 高#考#资#源# 内。
内。