题目内容
2.证明:$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{2n}$<1n2.(n∈N+).分析 将不等式的左边分子分母同除以n,可令$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$$\frac{1}{1+\frac{i}{n}}$•$\frac{1}{n}$=$\sum_{i=1}^{n}$$\frac{1}{1+\frac{i}{n}}$•$\frac{1}{n}$,再由积分${∫}_{0}^{1}$$\frac{1}{1+x}$dx,计算即可得证.
解答 证明:$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{2n}$=$\frac{\frac{1}{n}}{1+\frac{1}{n}}$+$\frac{\frac{1}{n}}{1+\frac{2}{n}}$+$\frac{\frac{1}{n}}{1+\frac{3}{n}}$+…+$\frac{\frac{1}{n}}{1+1}$
=$\sum_{i=1}^{n}$$\frac{1}{1+\frac{i}{n}}$•$\frac{1}{n}$,
可令$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$$\frac{1}{1+\frac{i}{n}}$•$\frac{1}{n}$=$\sum_{i=1}^{n}$$\frac{1}{1+\frac{i}{n}}$•$\frac{1}{n}$,
由$\underset{lim}{n→∞}$$\sum_{i=1}^{n}$$\frac{1}{1+\frac{i}{n}}$•$\frac{1}{n}$=${∫}_{0}^{1}$$\frac{1}{1+x}$dx=ln(1+x)|${\;}_{0}^{1}$=ln2-ln1=ln2.
由于n取不到∞,则有$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{2n}$<1n2.
点评 本题考查不等式的证明,注意变形,由极限思想求积分是解题的关键,考查运算能力,属于难题.

| A. | (0,4) | B. | (-4,0) | C. | [0,$\frac{15}{4}$) | D. | ($\frac{1}{2}$,2) |
| A. | (0,2) | B. | (1,2) | C. | [0,4) | D. | (1,4) |
| A. | 圆 | B. | 抛物线 | C. | 双曲线 | D. | 椭圆 |
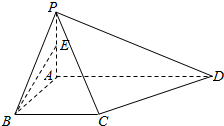 如图,在四棱锥P-ABCD中,∠DAB=∠ABC=90°,PA⊥平面ABCD,点E是PA的中点,AB=BC=1,AD=2.求证:
如图,在四棱锥P-ABCD中,∠DAB=∠ABC=90°,PA⊥平面ABCD,点E是PA的中点,AB=BC=1,AD=2.求证: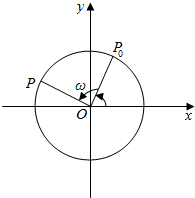 将自行车支起来,使后轮能平稳地匀速运动,观察后轮气针的运动规律?若将后轮入如图所示的坐标系中,轮胎以角速度ωrad/s做圆周运动,P0是气针的初始位置,气针到原点O的距离为rcm,求气针P的纵坐标关于时间t的函数关系式,并求出P的运动周期,当φ=$\frac{π}{6}$,r=ω=1时,作出其函数的图象.
将自行车支起来,使后轮能平稳地匀速运动,观察后轮气针的运动规律?若将后轮入如图所示的坐标系中,轮胎以角速度ωrad/s做圆周运动,P0是气针的初始位置,气针到原点O的距离为rcm,求气针P的纵坐标关于时间t的函数关系式,并求出P的运动周期,当φ=$\frac{π}{6}$,r=ω=1时,作出其函数的图象. 已知正四棱锥S-ABCD的底面边长为a,侧棱长为2a,点P,Q分别在BD和SC上,并且BP:PD=1:3,PQ∥平面SAD,求线段PQ的长.
已知正四棱锥S-ABCD的底面边长为a,侧棱长为2a,点P,Q分别在BD和SC上,并且BP:PD=1:3,PQ∥平面SAD,求线段PQ的长.