题目内容
12.已知等比数列{an}中,a5=16,a2,a7分别是方程x2+mx+128=0的两根.(1)求m的值以及数列{an}的前n项和Sn的表达式;
(2)若数列{bn}满足b1=1,2${\;}^{{b}_{n}}$=2${\;}^{{b}_{n-1}}$•an n≥2,求数列{an+bn-$\frac{1}{2}$n2}的前n项和Tn.
分析 (1)由已知利用韦达定理和等比数列通项公式列方程组得a1=1,q=2,由此能求出m的值以及数列{an}的前n项和Sn的表达式.
(2)由已知得bn=bn-1+n-1,利用累加法求出${{b}_{n}}^{\;}$=$\frac{n(n-1)}{2}+1$,由此利用分组求和法能求出数列{an+bn-$\frac{1}{2}$n2}的前n项和.
解答 解:(1)∵等比数列{an}中,a5=16,a2,a7分别是方程x2+mx+128=0的两根,
∴$\left\{\begin{array}{l}{{a}_{5}={a}_{1}{q}^{4}=16}\\{{a}_{2}•{a}_{7}={a}_{1}q•{a}_{1}{q}^{6}=128}\end{array}\right.$,
解得a1=1,q=2,
∴${a}_{2}=2,{a}_{7}={2}^{6}=64$,
∴m=a2+a7=66.
${S}_{n}=\frac{1×(1-{2}^{n})}{1-2}$=2n-1.
(2)∵a1=1,q=2,∴${a}_{n}={2}^{n-1}$,
∵{bn}满足b1=1,2${\;}^{{b}_{n}}$=2${\;}^{{b}_{n-1}}$•an,n≥2,
∴bn=bn-1+n-1,
∴${{b}_{n}}^{\;}$=b1+b2-b1+b3-b2+…+bn-bn-1
=1+1+2+3+…+n-1
=$\frac{n(n-1)}{2}+1$
∴an+bn-$\frac{1}{2}$n2=${2}^{n-1}+\frac{{n}^{2}}{2}-\frac{n}{2}+1-\frac{{n}^{2}}{2}$=${2}^{n-1}-\frac{n}{2}+1$,
∴数列{an+bn-$\frac{1}{2}$n2}的前n项和:
Tn=(1+2+22+…+2n-1)-$\frac{1}{2}$(1+2+3+…+n)-n
=$\frac{1-{2}^{n}}{1-2}$-$\frac{1}{2}×\frac{n(n+1)}{2}$-n
=${2}^{n}-\frac{n(n+1)}{4}-n-1$.
点评 本题考查数列的前n项和的求法,是中档题,解题时要注意韦达定理、等比数列的性质、累加求和法和分组求和法的合理运用.

 通城学典默写能手系列答案
通城学典默写能手系列答案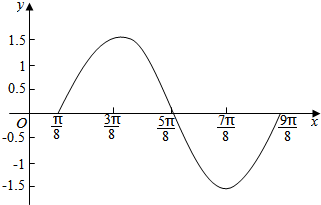 已知正弦型函数y=Asin(ωx+φ)的部分图象所示.写出函数的解析式.
已知正弦型函数y=Asin(ωx+φ)的部分图象所示.写出函数的解析式.