题目内容
已知向量 =(1,1),
=(1,1), =(1,0),<
=(1,0),< ,
, >=
>= 且
且 =-1;若△ABC的内角A,B,C依次成等差数列,且A≤B≤C;
=-1;若△ABC的内角A,B,C依次成等差数列,且A≤B≤C;
(1)若关于x的方程sin(2x+ )=
)= 在[0,B]上有相异实根,求实数m的取值范围;
在[0,B]上有相异实根,求实数m的取值范围;
(2)若向量 =(cosA,2cos2
=(cosA,2cos2  ),试求|
),试求|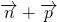 |的取值范围.
|的取值范围.
解:(1)∵2B=A+C 且A+B+C=π,∴B= . 令y=sin(2x+
. 令y=sin(2x+ ),x∈[0,
),x∈[0, ],则 2x+
],则 2x+ ∈[
∈[ ,π],∴
,π],∴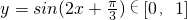 .
.
∵关于x的方程sin(2x+ )=
)= 在[0,
在[0, ]上有相异实根,所以y=sin(2x+
]上有相异实根,所以y=sin(2x+ )
)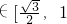 ),即
),即 ∈
∈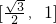
所以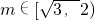 .
.
(2)令 =(x,y),∵
=(x,y),∵ =(1,1),
=(1,1), =-1,所以x+y=-1.
=-1,所以x+y=-1.
又 =(1,0),<
=(1,0),< ,
, >=
>= ,所以
,所以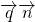 =0,即x=0,故y=-1,
=0,即x=0,故y=-1,
所以 =(0,-1),
=(0,-1), =(cosA,2cos2
=(cosA,2cos2  )=(cosA,1+cosC).
)=(cosA,1+cosC).
所以|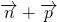 |2=cos2A+cos2C=cos2A+cos2(
|2=cos2A+cos2C=cos2A+cos2(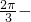 A)=1+
A)=1+ cos(2A+
cos(2A+ ).
).
由A∈(0,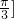 ,得2A+
,得2A+ ∈(
∈( ,π],得cos(2A+
,π],得cos(2A+ )∈[-1,
)∈[-1, ),
),
∴|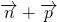 |2∈[
|2∈[ ,
, ),故|
),故|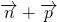 |∈[
|∈[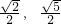 ).
).
分析:(1)由条件求得B= ,令y=sin(2x+
,令y=sin(2x+ ),由 x∈[0,
),由 x∈[0, ]求得y的值域,再由关于x的方程sin(2x+
]求得y的值域,再由关于x的方程sin(2x+ )=
)= 在[0,
在[0, ]上有相异实根,所以y=sin(2x+
]上有相异实根,所以y=sin(2x+ )
)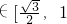 ),
),
由此求得 ∈
∈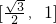 ,从而求得实数m的取值范围.
,从而求得实数m的取值范围.
(2)令 =(x,y),由条件
=(x,y),由条件 =-1可得x+y=-1.再由
=-1可得x+y=-1.再由 =(1,0),<
=(1,0),< ,
, >=
>= ,求得以
,求得以 和
和 的坐标,可得|
的坐标,可得|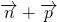 |2=1+
|2=1+ cos(2A+
cos(2A+ ),再由A的范围求出|
),再由A的范围求出|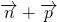 |的范围.
|的范围.
点评:本题主要考查两角和差的正弦公式,两个向量的数量积的公式,正弦函数的定义域和值域,求向量的模,属于中档题.
 . 令y=sin(2x+
. 令y=sin(2x+ ),x∈[0,
),x∈[0, ],则 2x+
],则 2x+ ∈[
∈[ ,π],∴
,π],∴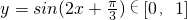 .
.∵关于x的方程sin(2x+
 )=
)= 在[0,
在[0, ]上有相异实根,所以y=sin(2x+
]上有相异实根,所以y=sin(2x+ )
)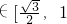 ),即
),即 ∈
∈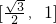
所以
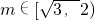 .
.(2)令
 =(x,y),∵
=(x,y),∵ =(1,1),
=(1,1), =-1,所以x+y=-1.
=-1,所以x+y=-1.又
 =(1,0),<
=(1,0),< ,
, >=
>= ,所以
,所以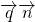 =0,即x=0,故y=-1,
=0,即x=0,故y=-1,所以
 =(0,-1),
=(0,-1), =(cosA,2cos2
=(cosA,2cos2  )=(cosA,1+cosC).
)=(cosA,1+cosC).所以|
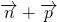 |2=cos2A+cos2C=cos2A+cos2(
|2=cos2A+cos2C=cos2A+cos2(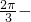 A)=1+
A)=1+ cos(2A+
cos(2A+ ).
).由A∈(0,
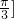 ,得2A+
,得2A+ ∈(
∈( ,π],得cos(2A+
,π],得cos(2A+ )∈[-1,
)∈[-1, ),
),∴|
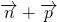 |2∈[
|2∈[ ,
, ),故|
),故|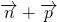 |∈[
|∈[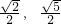 ).
).分析:(1)由条件求得B=
 ,令y=sin(2x+
,令y=sin(2x+ ),由 x∈[0,
),由 x∈[0, ]求得y的值域,再由关于x的方程sin(2x+
]求得y的值域,再由关于x的方程sin(2x+ )=
)= 在[0,
在[0, ]上有相异实根,所以y=sin(2x+
]上有相异实根,所以y=sin(2x+ )
)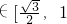 ),
),由此求得
 ∈
∈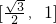 ,从而求得实数m的取值范围.
,从而求得实数m的取值范围.(2)令
 =(x,y),由条件
=(x,y),由条件 =-1可得x+y=-1.再由
=-1可得x+y=-1.再由 =(1,0),<
=(1,0),< ,
, >=
>= ,求得以
,求得以 和
和 的坐标,可得|
的坐标,可得|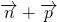 |2=1+
|2=1+ cos(2A+
cos(2A+ ),再由A的范围求出|
),再由A的范围求出|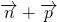 |的范围.
|的范围.点评:本题主要考查两角和差的正弦公式,两个向量的数量积的公式,正弦函数的定义域和值域,求向量的模,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目