题目内容
给出下列四个命题,正确的命题是
①定义在R上的函数f(x),函数y=f(x-1)与y=f(1-x)的图象关于y轴对称;
②若f(x)=9x-(k+1)3x+1>0恒成立,则k的范围是(-∞,1);
③已知f(x)=1+log2x(1≤x≤16),则函数y=f2(x)+f(x2)的值域是[2,34];
④[x]表示不超过x的最大整数,当x是整数时[x]就是x,这个函数y=[x]叫做“取整函数”.那么[log21]+[log22]+[log23]+[log24]+…+[log2128]=649.
②④
②④
;①定义在R上的函数f(x),函数y=f(x-1)与y=f(1-x)的图象关于y轴对称;
②若f(x)=9x-(k+1)3x+1>0恒成立,则k的范围是(-∞,1);
③已知f(x)=1+log2x(1≤x≤16),则函数y=f2(x)+f(x2)的值域是[2,34];
④[x]表示不超过x的最大整数,当x是整数时[x]就是x,这个函数y=[x]叫做“取整函数”.那么[log21]+[log22]+[log23]+[log24]+…+[log2128]=649.
分析:由函数图象关于直线对称的公式,可得①不正确;
用换元法结合二次函数求最值的方法,可得f(x)=9x-(k+1)3x+1>0恒成立,则k的范围是(-∞,1),故②正确;
对于③,首先y=f2(x)+f(x2)的定义域为:x∈[1,4],然后用二次函数求最闭区间上最值的方法可得函数y=f2(x)+f(x2)的值域是[2,14],得到③不正确;
根据取整函数的定义,可得[log21]+[log22]+[log23]+[log24]+…+[log2128]=0+2×1+4×2+8×3+16×4+32×5+64×6+7=649,故④正确.
用换元法结合二次函数求最值的方法,可得f(x)=9x-(k+1)3x+1>0恒成立,则k的范围是(-∞,1),故②正确;
对于③,首先y=f2(x)+f(x2)的定义域为:x∈[1,4],然后用二次函数求最闭区间上最值的方法可得函数y=f2(x)+f(x2)的值域是[2,14],得到③不正确;
根据取整函数的定义,可得[log21]+[log22]+[log23]+[log24]+…+[log2128]=0+2×1+4×2+8×3+16×4+32×5+64×6+7=649,故④正确.
解答:解:对于①,函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称,而不是关于y轴对称,故①不正确;
对于②,令t=3x,f(x)=g(t)=t2-(k+1)t+1在t>0时函数值恒为正数
(1)当k≤-1时,函数最小值为g(0)=1>0,符合题意;
(2)当k>-1时,函数最小值为g(
)=-
+1>0,解之得-1<k<1
综上所述,可得若f(x)=9x-(k+1)3x+1>0恒成立,则k的范围是(-∞,1),故②正确;
对于③,y=f2(x)+f(x2)的定义域满足:1≤x≤16且1≤x2≤16,可得x∈[1,4]
∴y=f2(x)+f(x2)=log22x+4log2x+2,其中log2x∈[0,2]
可得当log2x=0时,y的最小值为2,当log2x=2时,y的最大值为14,
因此函数y=f2(x)+f(x2)的值域是[2,14],故③不正确;
对于④,根据取整函数的定义,可得[log21]=0,[log22]=[log23]=1,[log24]=[log25]=[log26]=[log27]=2,
[log28]=[log29]=[log210]=[log211]=[log212]=[log213]=[log214]=[log215]=3,…,依此类推,可得
[log21]+[log22]+[log23]+[log24]+…+[log2128]=0+2×1+4×2+8×3+16×4+32×5+64×6+7=649,故④正确.
对于②,令t=3x,f(x)=g(t)=t2-(k+1)t+1在t>0时函数值恒为正数
(1)当k≤-1时,函数最小值为g(0)=1>0,符合题意;
(2)当k>-1时,函数最小值为g(
| k+1 |
| 2 |
| (k+1)2 |
| 4 |
综上所述,可得若f(x)=9x-(k+1)3x+1>0恒成立,则k的范围是(-∞,1),故②正确;
对于③,y=f2(x)+f(x2)的定义域满足:1≤x≤16且1≤x2≤16,可得x∈[1,4]
∴y=f2(x)+f(x2)=log22x+4log2x+2,其中log2x∈[0,2]
可得当log2x=0时,y的最小值为2,当log2x=2时,y的最大值为14,
因此函数y=f2(x)+f(x2)的值域是[2,14],故③不正确;
对于④,根据取整函数的定义,可得[log21]=0,[log22]=[log23]=1,[log24]=[log25]=[log26]=[log27]=2,
[log28]=[log29]=[log210]=[log211]=[log212]=[log213]=[log214]=[log215]=3,…,依此类推,可得
[log21]+[log22]+[log23]+[log24]+…+[log2128]=0+2×1+4×2+8×3+16×4+32×5+64×6+7=649,故④正确.
点评:本题以命题真假的判断为载体,着重考查了函数图象的对称性、二次函数求闭区间上的最值和取整函数的应用等知识点,属于基础题.

练习册系列答案
相关题目
 14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题:
14、如图,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线Ox、Oy、Oz上,给出下列四个命题: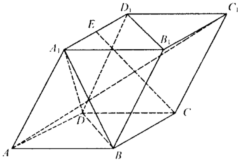 (2008•成都三模)已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD,E为A1D1的中点.给出下列四个命题:①∠BCC1为异面直线AD与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
(2008•成都三模)已知平行六面体ABCD-A1B1C1D1中,∠A1AD=∠A1AB=∠BAD=60°,AA1=AB=AD,E为A1D1的中点.给出下列四个命题:①∠BCC1为异面直线AD与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④