题目内容
【题目】一幅标准的三角板如图1中,![]() 为直角,
为直角,![]() ,
,![]() 为直角,
为直角,![]() ,且
,且![]() ,把
,把![]() 与
与![]() 拼齐使两块三角板不共面,连结
拼齐使两块三角板不共面,连结![]() 如图2.
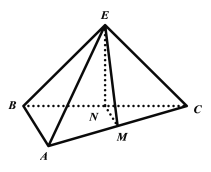
如图2.

(1)若![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)在《九章算术》中,称四个面都是直角三角形的三棱锥为“鳖臑”,若图2中![]() ,三棱锥
,三棱锥![]() 的体积为2,则图2是否为鳖臑?说明理由.
的体积为2,则图2是否为鳖臑?说明理由.
【答案】(1)证明见解析;(2)是鳖臑,详见解析.
【解析】
(1)设![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() ,可证
,可证![]() 、
、![]() ,从而得到
,从而得到![]() 平面
平面![]() .
.
(2)先求出![]() ,再根据体积可得
,再根据体积可得![]() 到平面
到平面![]() 的距离为
的距离为![]() ,结合
,结合![]() 可得
可得![]() 平面
平面![]() ,从而可证四个面均为直角三角形.
,从而可证四个面均为直角三角形.
(1)证明:设![]() 中点为
中点为![]() ,连结
,连结![]() ,
,![]() .
.
∵![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
(2)此时三棱锥![]() 是鳖臑,
是鳖臑,
∵![]() ,
,![]() ,
,
又三棱锥的体积![]() ,故高
,故高![]() .
.
又∵![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() 是直角.
是直角.
同理,![]() .
.
∵![]() ,
,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,故
,故![]() 也是直角.
也是直角.
又![]() ,
,![]() 显然是直角,故图2是鳖臑.
显然是直角,故图2是鳖臑.

练习册系列答案
相关题目

