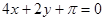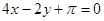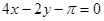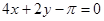题目内容
已知曲线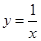 和
和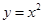 相交于点A,
相交于点A,
(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线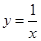 在A点处的切线及
在A点处的切线及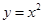 以及
以及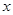 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)
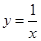 和
和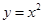 相交于点A,
相交于点A,(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线
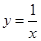 在A点处的切线及
在A点处的切线及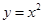 以及
以及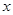 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)(1) 曲线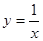 和
和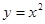 在它们的交点坐标是(1,1), ( 4 分 )
在它们的交点坐标是(1,1), ( 4 分 )
(2) 两条切线方程分别是x+y-2=0和2x-y-1=0, ( 4 分 )
(3) 图形面积是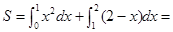
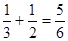 .
.
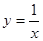 和
和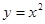 在它们的交点坐标是(1,1), ( 4 分 )
在它们的交点坐标是(1,1), ( 4 分 ) (2) 两条切线方程分别是x+y-2=0和2x-y-1=0, ( 4 分 )
(3) 图形面积是
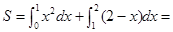
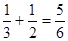 .
.本试题主要考察了导数的几何意义的运用,以及利用定积分求解曲边梯形的面积的综合试题。先确定切点,然后求解斜率,最后得到切线方程。而求解面积,要先求解交点,确定上限和下限,然后借助于微积分基本定理得到。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
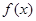 在
在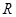 上可导,且
上可导,且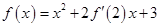 ,则( )
,则( )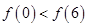
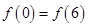
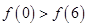
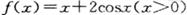 满足在点
满足在点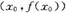 处的切线与x轴平行,若将所有满足条件的切点的横坐标由小到大依次排列构成数列
处的切线与x轴平行,若将所有满足条件的切点的横坐标由小到大依次排列构成数列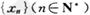 ,则数列{xn}的前4项和为_______.
,则数列{xn}的前4项和为_______.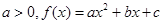 ,曲线
,曲线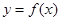 在
在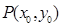 处切线的倾斜角的取值范围是
处切线的倾斜角的取值范围是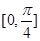 ,则
,则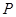 到曲线
到曲线
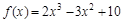 的单调递减区间为
的单调递减区间为 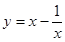 在点
在点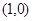 处的切线方程。
处的切线方程。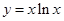 在点
在点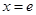 处的切线的斜率是
处的切线的斜率是 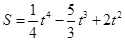 (
(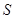 的单位为
的单位为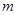 ,
,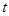 的单位为
的单位为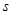 ),则物体速度为0的时刻是 .
),则物体速度为0的时刻是 .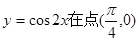 处的切线方程是
处的切线方程是