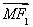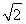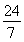题目内容
等比数列{cn}满足cn＋1＋cn＝10·4n－1(n∈N*)，数列{an}的前n项和为Sn，且an＝log2cn.
(1)求an，Sn；
(2)数列{bn}满足bn＝
，Tn为数列{bn}的前n项和，是否存在正整数m(m>1)，使得T1，Tm，T6m成等比数列？若存在，求出所有m的值；若不存在，请说明理由．
（1）an＝2n－1，Sn＝n2.（2）存在正整数m＝2，使得T1，Tm，T6m成等比数列．
【解析】(1)因为c1＋c2＝10，c2＋c3＝40，所以公比q＝4，
由c1＋4c1＝10，得c1＝2，cn＝2·4n－1＝22n－1，
所以an＝log222n－1＝2n－1.
Sn＝a1＋a2＋…＋an＝log2c1＋log2c2＋…＋log2cn＝log2(c1·c2·…·cn)＝log2(21·23·…·22n－1)＝log22(1＋3＋…＋2n－1)＝n2.
(2)由(1)知bn＝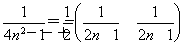
，
于是Tn＝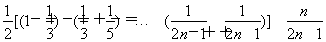
.
假设存在正整数m(m>1)，使得T1，Tm，T6m成等比数列，则
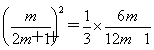，整理得4m2－7m－2＝0，
解得m＝－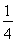
或m＝2.
由m∈N*，m>1，得m＝2.
因此存在正整数m＝2，使得T1，Tm，T6m成等比数列．
练习册系列答案
相关题目
