题目内容
【题目】已知f（x）＝|2x﹣1|﹣|2x+1|.
（1）求不等式f（x）＞1的解集.
（2）当
时，求证：4x2+4x+2＞（2x+1）f（x）.
【答案】（1）
；（2）见解析
【解析】
（1）
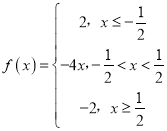，再根据分段函数，即可求出不等式
的解集;
（2）要证明
，只要证
，根据绝对值三角不等式和基本不等式即可证明．
(1)f(x)＝|2x﹣1|﹣|2x+1|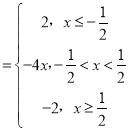
，
当
，f(x)＝2>1恒成立，
当
，f(x)＝﹣4x>1，解得
，
综上所述不等式f(x)>1的解集为(﹣∞，
).
证明(2)∵
，
∴2x+1>0，
要证4x2+4x+2>(2x+1)f(x)，
只要证f(x)
(2x+1)
，
∵(2x+1)
2
2，当且仅当x＝0时取等号，
f(x)＝|2x﹣1|﹣|2x+1|≤|(2x﹣1)﹣(2x+1)|＝2，
∴f(x)
恒成立，
∴4x2+4x+2>(2x+1)f(x).
练习册系列答案
高中必刷题系列答案
相关题目
