题目内容
给定圆C:x2+y2=4,过点P(1,0)作两条互相垂直的直线与C分别交于A、B和M,N,则
+
的最大值是
.
| |AB| |
| |MN| |
| |MN| |
| |AB| |
7
| ||
| 6 |
7
| ||
| 6 |
分析:由圆C的方程找出圆心C的坐标和半径r,设出直线AB的斜率为k,根据两直线垂直时斜率的乘积为-1,得到直线MN的斜率为-
,由两直线都过P点,进而分别表示出两直线的方程,利用点到直线的距离公式分别求出圆心到两直线的距离d1和d2,由垂径定理得到垂足为中点,由弦心距,半径,利用勾股定理求出弦的一半,进而表示出|AB|和|MN|,得出|AB|2+|MN|2的值为定值,再表示出|MN|•|AB|,变形后求出|MN|•|AB|的最小值,把所求的式子通分后,将求出的|AB|2+|MN|2的值及|MN|•|AB|的最小值代入,即可求出所求式子的最大值.
| 1 |
| k |
解答:解:由圆的方程x2+y2=4,得到圆心坐标为(0,0),半径r=2,
设直线AB的方程为:y=k(x-1),即kx-y-k=0,
则直线MN的方程为:y=-
(x-1),即x+ky-1=0,
∴圆心到直线AB的距离d1=
,到直线MN的距离d2=
,
∴|AB|=2
=2
,|MN|=2
=2
,
∵|MN|•|AB|=4
=4
=4
≥4
=8
,
∴(|MN|•|AB|)min=8
,
∵|AB|2+|MN|2=4(
+
)=
=28,
∴
+
=
=
,
当(|MN|•|AB|)min=8
时,
则(
+
)max=
=
.
故答案为:
设直线AB的方程为:y=k(x-1),即kx-y-k=0,
则直线MN的方程为:y=-
| 1 |
| k |
∴圆心到直线AB的距离d1=
| |k| | ||
|
| 1 | ||
|
∴|AB|=2
| r2-d12 |
|
| r2-d22 |
|
∵|MN|•|AB|=4
|
=4
|
12+
|
| 12 |
| 3 |
∴(|MN|•|AB|)min=8
| 3 |
∵|AB|2+|MN|2=4(
| 4+3k2 |
| 1+k2 |
| 3+4k2 |
| 1+k2 |
| 28(1+k2) |
| 1+k2 |
∴
| |AB| |
| |MN| |
| |MN| |
| |AB| |
| |AB|2+|MN|2 |
| |MN|•|AB| |
| 28 |
| |MN|•|AB| |
当(|MN|•|AB|)min=8
| 3 |
则(
| |AB| |
| |MN| |
| |MN| |
| |AB| |
| 28 | ||
8
|
7
| ||
| 6 |
故答案为:
7
| ||
| 6 |
点评:此题考查了直线与圆相交的性质,涉及的知识有:垂径定理,勾股定理,两直线垂直时斜率满足的关系,直线的一般式方程,以及圆的标准方程,其中得出|AB|2+|MN|2的值为定值,同时求出|MN|•|AB|的最小值是解本题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
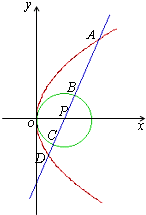 (2013•惠州模拟)给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线l,此直线与上述两曲线的四个交点,自上而下顺次记为A、B、C、D,如果线段AB、BC、CD的长按此顺序构成一个等差数列,求直线l的方程.
(2013•惠州模拟)给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线l,此直线与上述两曲线的四个交点,自上而下顺次记为A、B、C、D,如果线段AB、BC、CD的长按此顺序构成一个等差数列,求直线l的方程.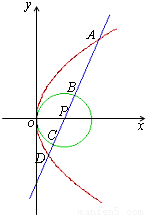
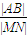 +
+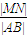 的最大值是 .
的最大值是 .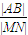 +
+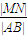 的最大值是 .
的最大值是 .