题目内容
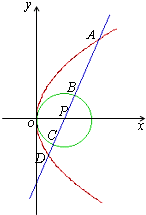 (2013•惠州模拟)给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线l,此直线与上述两曲线的四个交点,自上而下顺次记为A、B、C、D,如果线段AB、BC、CD的长按此顺序构成一个等差数列,求直线l的方程.
(2013•惠州模拟)给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线l,此直线与上述两曲线的四个交点,自上而下顺次记为A、B、C、D,如果线段AB、BC、CD的长按此顺序构成一个等差数列,求直线l的方程.分析:先确定圆P的标准方程,求出圆心与直径长,设出l的方程,代入抛物线方程,求出|AD|,利用线段AB、BC、CD的长按此顺序构成一个等差数列,可得|AD|=3|BC|,求出k的值,由此可求直线l的方程.
解答: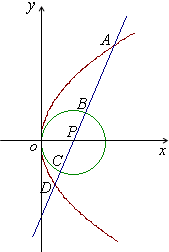 解:圆P的方程为(x-1)2+y2=1,则其直径长|BC|=2,圆心为P(1,0),
解:圆P的方程为(x-1)2+y2=1,则其直径长|BC|=2,圆心为P(1,0),
设l的方程为ky=x-1,即x=ky+1,代入抛物线方程得:y2=4ky+4,
设A(x1,y1),D(x2,y2),
有
,…(2分)
则(y1-y2)2=(y1+y2)2-4y1y2=16(k2+1).…(4分)
故|AD|2=(y1-y2)2+(x1-x2)2=(y1-y2)2+(
)2
=(y1-y2)2[1+(
)2]=16(k2+1)2,…(7分)
因此|AD|=4(k2+1).…(8分)
因为线段AB、BC、CD的长按此顺序构成一个等差数列,…(10分)
所以|AD|=3|BC|,即4(k2+1)=6
∴k=±
…(12分)
∴l方程为
x-y-
=0或
x+y-
=0.…(14分)
 解:圆P的方程为(x-1)2+y2=1,则其直径长|BC|=2,圆心为P(1,0),
解:圆P的方程为(x-1)2+y2=1,则其直径长|BC|=2,圆心为P(1,0),设l的方程为ky=x-1,即x=ky+1,代入抛物线方程得:y2=4ky+4,
设A(x1,y1),D(x2,y2),
有
|
则(y1-y2)2=(y1+y2)2-4y1y2=16(k2+1).…(4分)
故|AD|2=(y1-y2)2+(x1-x2)2=(y1-y2)2+(
| ||||
| 4 |
=(y1-y2)2[1+(
| y1+y2 |
| 4 |
因此|AD|=4(k2+1).…(8分)
因为线段AB、BC、CD的长按此顺序构成一个等差数列,…(10分)
所以|AD|=3|BC|,即4(k2+1)=6
∴k=±
| ||
| 2 |
∴l方程为
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查直线与圆、抛物线的位置关系,考查等差数列,考查学生的计算能力,确定|AD|是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目