题目内容
【题目】如图线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线. 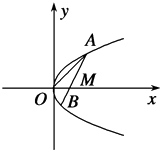
(1)求抛物线方程;
(2)若 ![]() =﹣1,求m的值.
=﹣1,求m的值.
【答案】
(1)解:可设抛物线方程为y2=2px(p>0),
设直线AB的方程为y=k(x﹣m)(k≠0)
联立这两个方程组消去x得,ky2﹣2py﹣2pkm=0,
设A(x1,y1),B(x2,y2),
由已知得|y1||y2|=2m,注意到y1y2<0,∴y1y2=﹣2m,
又y1y2=﹣2pm,∴﹣2m=﹣2pm,∵m>0,∴p=1.
∴抛物线方程为y2=2x
(2)解:设A(x1,y1),B(x2,y2),
则 ![]() =(x1,y1),
=(x1,y1), ![]() =(x2,y2).
=(x2,y2).
则 ![]() =x1x2+y1y2=+y1y2=m2﹣2m.
=x1x2+y1y2=+y1y2=m2﹣2m.
又 ![]() =﹣1,
=﹣1,
∴m2﹣2m=﹣1,解得m=1
【解析】(1)设抛物线方程为y2=2px(p>0),设直线AB的方程为y=k(x﹣m)(k≠0),联立这两个方程组,得ky2﹣2py﹣2pkm=0,由此利用韦达定理结合已知条件能求出抛物线方程.(2)设A(x1 , y1),B(x2 , y2),则 ![]() =x1x2+y1y2=+y1y2=m2﹣2m,由此能求出m.
=x1x2+y1y2=+y1y2=m2﹣2m,由此能求出m.

练习册系列答案
相关题目