题目内容
【题目】已知等比数列 ![]() 的公比
的公比 ![]() ,且
,且 ![]() ,
, ![]() .
.
(Ⅰ)求数列 ![]() 的通项公式;
的通项公式;
(Ⅱ)设 ![]() ,
, ![]() 是数列
是数列 ![]() 的前
的前 ![]() 项和,对任意正整数
项和,对任意正整数 ![]() ,不等式
,不等式 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)设数列 ![]() 的公比为
的公比为 ![]() ,则
,则 ![]() ,
,
∴ ![]()
∵ ![]() ,∴
,∴ ![]() ,∴数列
,∴数列 ![]() 的通项公式为
的通项公式为 ![]() .
.
(Ⅱ)解: ![]()
∴ ![]()
![]()
![]()
∴ ![]()
∴ ![]() =
= 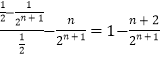
∴ ![]() 对任意正整数
对任意正整数 ![]() 恒成立,设
恒成立,设 ![]() ,易知
,易知 ![]() 单调递增.
单调递增. ![]() 为奇数时,
为奇数时, ![]() 的最小值为
的最小值为 ![]() ,∴
,∴ ![]() 得
得 ![]() ,
,
![]() 为偶数时,
为偶数时, ![]() 的最小值为
的最小值为 ![]() ,∴
,∴ ![]() ,
,
综上, ![]() ,即实数
,即实数 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)根据等比数列的通项公式an=a1qn-1将已知条件中的a3和a2分别用a1、q表示,求出a1和q,从而可求出an;(2)利用错位相减法求和法求出Sn,构造函数f(n)=Sn+![]() ,将Sn代入并化简,然后根据n的奇偶分别求出f(n)的最小值.
,将Sn代入并化简,然后根据n的奇偶分别求出f(n)的最小值.
【考点精析】本题主要考查了等比数列的通项公式(及其变式)和数列的前n项和的相关知识点,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系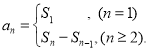 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目